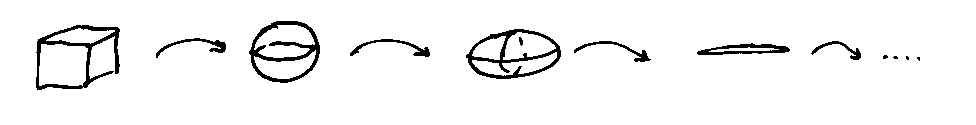Visualisierung dynamischer Systemeoder: Wie nützlich ist der Phasenraum?von:
MNU Giessen 16.9.98
Einleitung
EinleitungIm folgenden sollen einige Gedanken vorgetragen werden, die im Zusammenhang mit nicht-linearen dynamischen Systemen (chaotischen Systemen) stehen. Bei der Behandlung solcher Systeme finden Konzepte Anwendung, die auch für den Physikunterricht der SII Bedeutung haben können. Insbesondere das Konzept des Phasenraums kann bei der Bewältigung einiger mathematischer Schwierigkeiten hilfreich sein, da es ohne grundlegende Kenntnisse der Analysis auf anschauliche Weise die dynamischen Eigenschaften physikalischer Systeme begreiflich macht.Die Grundlagen der Newtonschen Mechanik sollen in folgendem Umfang vorausgesetzt werden: - Kinematik und Dynamik des Massenpunktes - gleichförmige Bewegung - gleichförmig beschleunigte Bewegung Differentialquotienten und ein strenger Grenzwertbegriff sind für
das Folgende nicht erforderlich. Es genügt, dass der Schüler
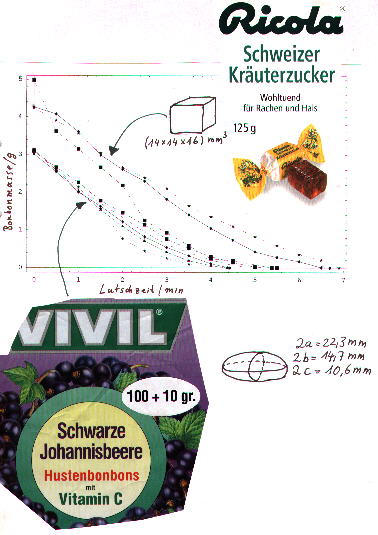
weiß, dass bei der praktischen Verwendung der Definitionen - Newtonsche Gleichung: Diese Gleichung beschreibt das dynamische Verhalten eines mechanischen Systems. Die äußeren Bedingungen ("Kräfte") sind die Ursache der Geschwindigkeitsänderungen. Dies ist bekanntlich eine allgemeine Differentialgleichung (DGL) 2. Ordnung für die Funktion s(t), oder, in mehr als einer Dimension, ein Differentialgleichungssystem 2. Ordnung. Wir werden versuchen, solche DGLen ohne den sonst notwendigen Apparat der Analysis zu lösen. Eine Differentialgleichung 1. Ordnung Es ist sinnvoll, das Verfahren zunächst an einer DGL 1. Ordnung zu erläutern und einzuüben. DGLen 1. Ordnung treten in der Physik nicht sehr häufig auf. Wir analysieren daher ein System, von dem wir hoffen, dass es in der vorwissenschaftlichen Erfahrung der Schüler schon einmal aufgetaucht ist, nämlich: Die flüssigkeitsbedingte Oberflächenablation sphärischer Saccharoseproben Es handelt sich hierbei um das so genannte Bonbon-Problem :
Ersichtlich ist der Genuss proportional zur im Zeitintervall Dt
abgelutschten Bonbonmasse Dm. Da diese Masse
durch die Oberfläche abtransportiert wird, ist sie (bei konstanter
"Lutschkraft") proportional zur Oberfläche des Bonbons: Dm
~ A. Die Oberfläche ihrerseits ist proportional zu r2 ,
bei konstanter Form ist r ~ Volumen 1/3 und bei
konstanter Dichte V ~ m, insgesamt also:
Eine solche DGL läßt sich bei bekanntem l
und einem vorgegebenen Anfangswert für m grafisch lösen. Die
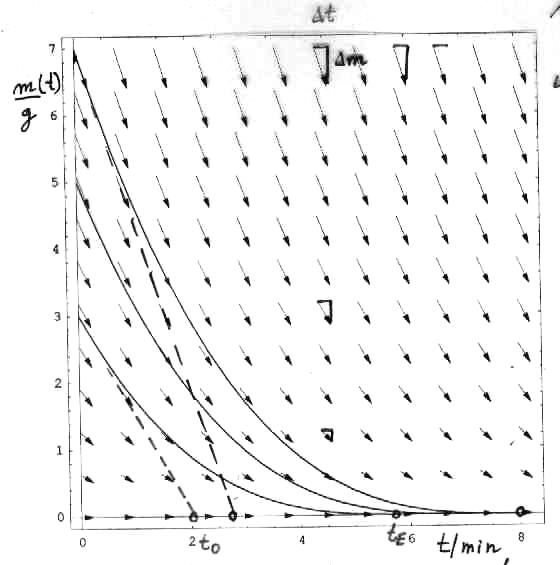
Methode erläutert das folgende Pfeilsystem.
Es ist ein Pfeilsystem im t-m-Diagramm, das nach der Lösung der DGL die Kurve m(t) enthalten soll. Startet man auf der m-Achse bei t = 0 mit einem Wert Anfangswert m(0) = m0, dann berechnet sich der neue Wert von m nach einer Zeit Dt zu m(Dt ) = m0 + Dm, wobei Dm mit der obigen Gleichung berechnet wird. Der Wert von Dm hängt nur von l und m selbst ab. Der aus Dt und Dm resultierende Vektorpfeil muss tangential zur Lösungskurve liegen. Die grafische Lösung der DGL besteht also darin, eine Kurve zu zeichnen, die vom Punkt (0 | m0 ) ausgeht und ständig in Richtung des Pfeilsystems verläuft, der sozusagen als "Wegweiser" dient. Das vorliegende Pfeilsystem wurde mit einem Wert von l = 0.7 g 5/2 min -1 berechnet. Je feiner man das System zeichnet, desto genauer werden natürlich die Ergebnisse. Man gibt jedem Schüler ein solches vorgefertigtes Blatt und lässt für verschiedenen Anfangswerte die Kurven zeichnen. Als "Auswertung" kann man nun z.B. nach Gemeinsamkeiten der verschiedenen m(t)-Kurven forschen. Man kann z.B. die Endzeit te bestimmen, bei der die Masse Null wird. Ebenso kann man die Zeit t0 bestimmen, die der Lutschvorgang dauern würde, würde man mit der Anfangsgeschwindigkeit (dm/dt)0 kontinuierlich weiterlutschen. Man stellt fest, dass die tatsächliche Lutschzeit te
etwa dreimal so groß ist wie die Zeit t0.
Als "Lutschverlängerungsfaktor" LVF = te /t0
erhält
man also etwa LFV = 3. Natürlich ist die
vorliegende DGL einfach genug, um sie direkt zu lösen:
Sicher brennen Lehrer und Schüler jetzt darauf, diese elegante Theorie auch experimentell zu verifizieren. Mit zwei verschiedenen Bonbontypen (kubisch und ellipsoid) wurden daher Lutschversuche unternommen, deren Ergebnisse hier dargestellt sind:
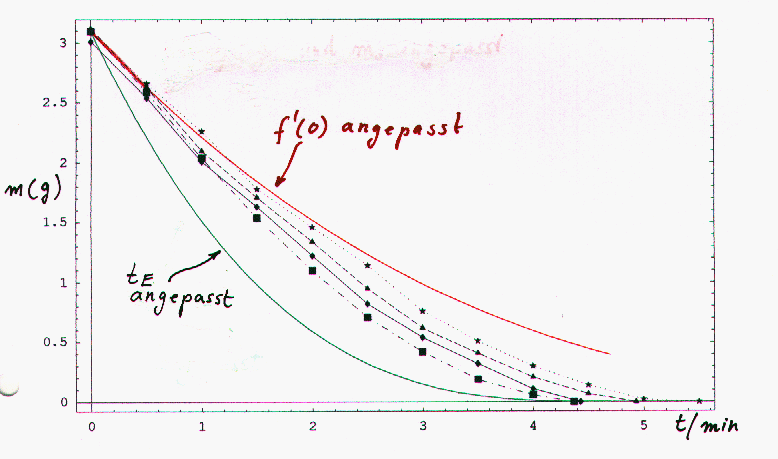
Hier wurden die Vivil-Kurven nochmals gegen t aufgetragen:
Der experimentell ermittelte LVF beträgt etwa 1.5. m(t) folgt daher
unserem einfachen theoretischen Modell nur schlecht, was natürlich
zu physik-typischen Diskussionen führt:
dann sind die Koeffizienten c selbst zeitabhängig.
|
und 
die
Genauigkeit bei Berechnungen um so besser wird je kleiner die Schrittweite
gewählt wird.
.
.
.
,
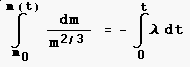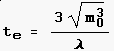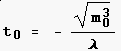also in der Tat LVF = te / t0
= 3.
