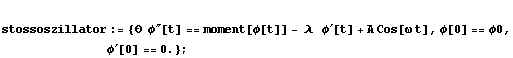Das Pohlsche Pendel mit Unwucht

Experimentell steht uns im Physikunterricht als bester und kontrollierbarster Oszillator das Pohl-Pendel zur Verfügung. Sowohl die Anregung als auch die Dämpfung dieses Drehpendels lassen sich stufenlos und genau regulieren. 
Es bleibt also die Einführung einer Nicht-Linearität. Diese lässt sich z.B. durch die Einführung einer Unwucht erreichen.  Das Pendel bekommt dadurch zwei neue Gleichgewichtslagen, um die es in einem nicht-harmonischen Potential schwingen kann:
 

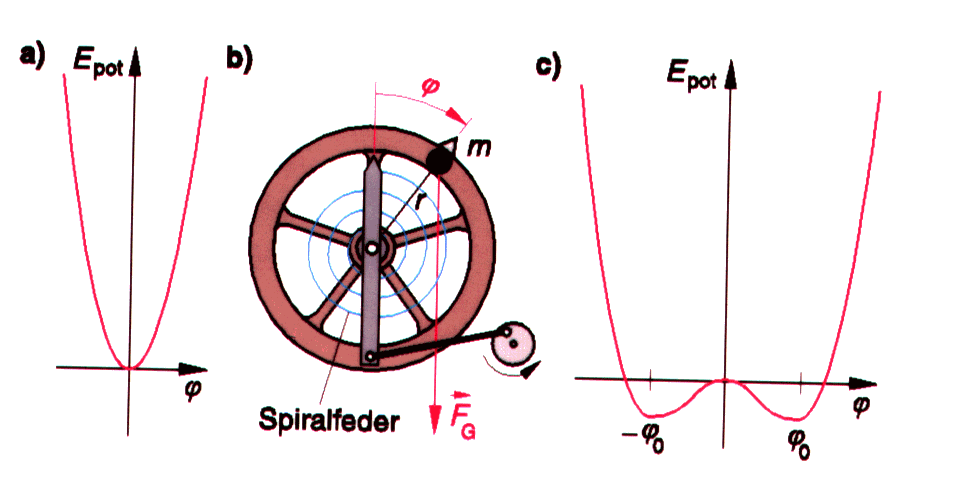
Die Nicht-Linearität ist dabei um so größer, je näher das Pendel dem kritischen Punkt bei 
f = 0 kommt. Diese Tatsache bedingt auch die experimentelle Schwierigkeit des Systems. Will man das Feigenbaum-Szenario demonstrieren, dann muss das Pendel im selben Potentialtopf bleiben, was mit Annäherung an den Nullpunkt immer schwieriger zu erreichen ist.  Die folgenden experimentellen Resultat, die mir freundlicherweise von Frl. Dorothea Brüggemann aus Bonn (aus ihrer Jugend-Forscht-Arbeit von 1998) zur Verfügung gestellt wurden, illustrieren das. Aufgezeichnet wurden jeweils die f(t)-Kurven (oben) und die f(w)-Kurven (unten). 

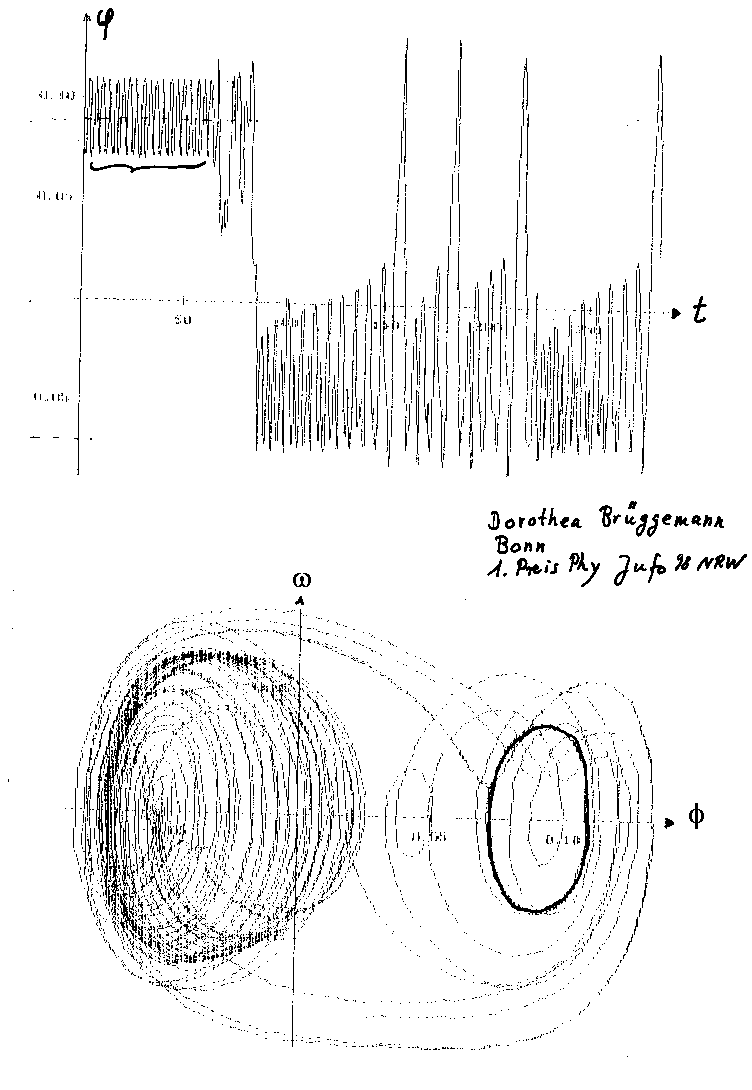
Hier verweilt das System nur kurze Zeit auf einer Seite, springt dann auf die andere Seite  und  danach  mehrmals unkontrolliert hin und her:

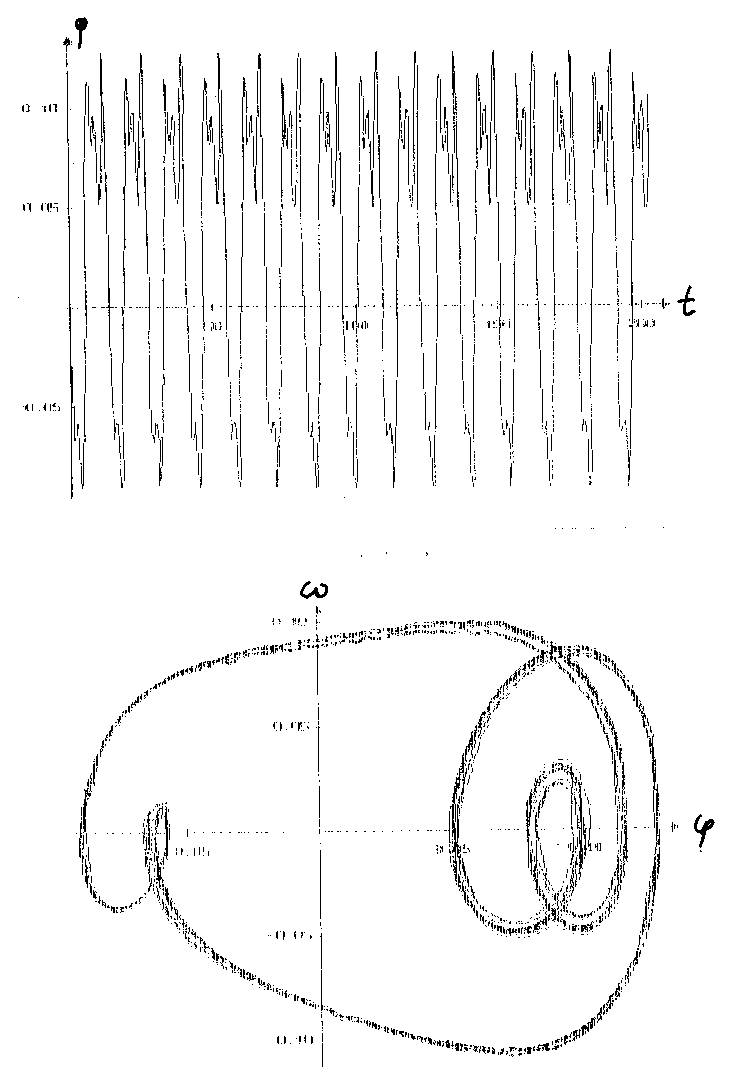
Beim nächsten Experiment springt das Pendel regelmäßig zwischen den beiden Potentialmulden hin und her:

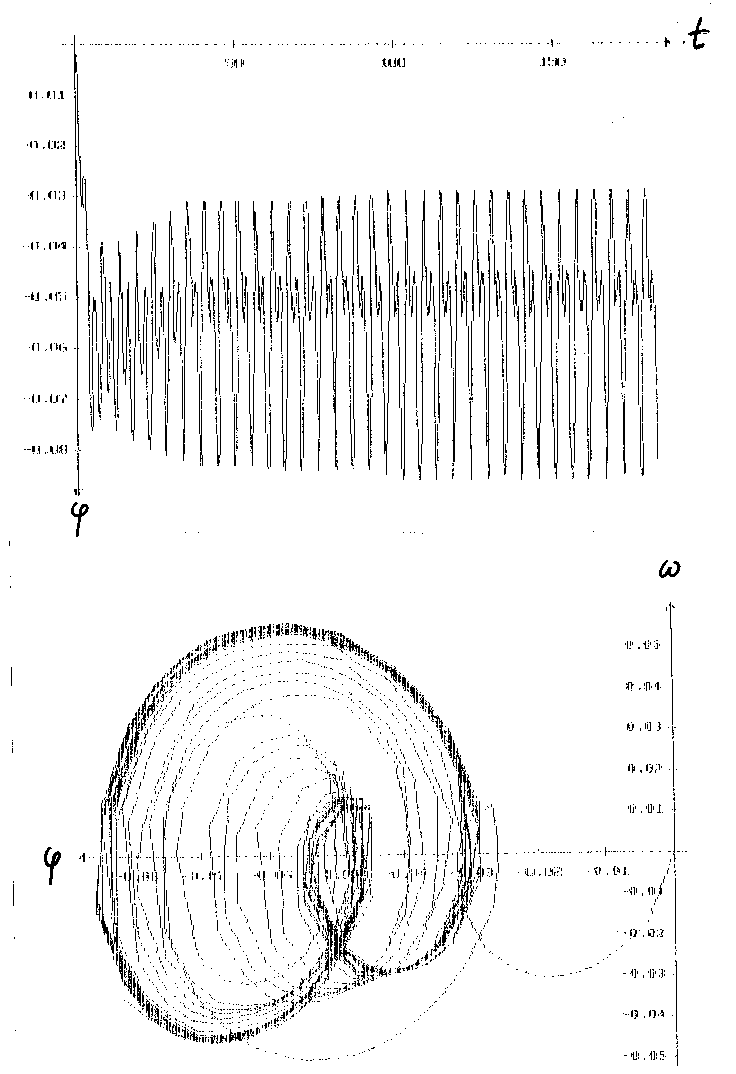
Erst hier sieht man einen stabilen Zweierzyklus, der den Beginn des Feigenbaum.Szenarios markiert: 
 
 

Die Beobachtung stabiler Vierer- oder gar höherer Zyklen gelingt fast nicht.

Abhilfe schafft eine Idee, die auf James S. Walker zurückgeht (P.A. Tipler, Physik, Spektrum-Verlag Heidelberg): Dort wird im Essay „Chaos" der so genannte „Benderoszillator" beschrieben: 

 

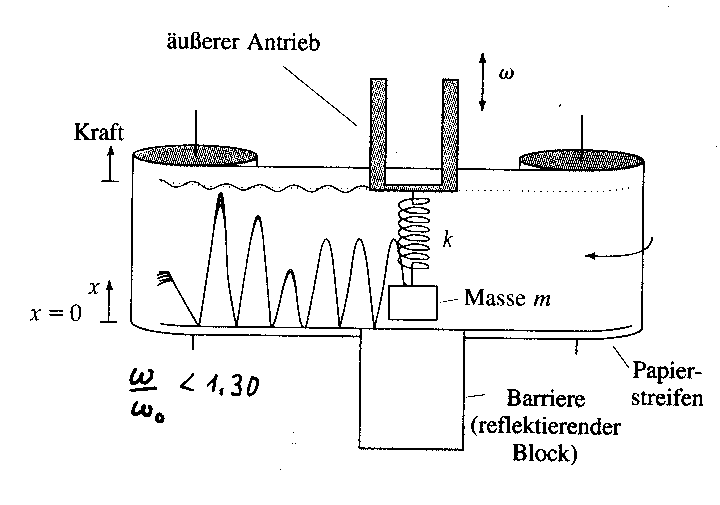
Ein Federpendel soll zu erzwungenen Schwingungen angeregt werden, wobei im Nullpunkt der Bewegung eine ideal reflektierende Barriere angebracht wird. Die von Walker angeführten Berechnungen zeigen, dass das System tatsächlich Chaos zeigt. Als experimentelle Anleitung sind die Skizzen aber kaum gedacht. Ich habe diesen „Reflexoszillator" daher mit Hilfe des Pohl-Pendels verwirklicht: 
 

In den Nullpunkt setze man als Reflektor eine der Federn, die normalerweise die Amplitude des Pendels begrenzen. Die unten beschriebenen Erscheinungen lassen sich am besten bei kräftiger Anregung und relativ starker Dämpfung beobachten. Ich habe daher die Exzenterstange verlängert und sie weiter oben in einer zusätzlichen Bohrung der Antriebsstange befestigt. Man kann dafür einfach ein Stück Gewindestab nehmen. Die Experimente wurden mit einem Dämpfungsstrom von ca. 0.8A gemacht. 
 
 

Zur Theorie des Pohlschen Stossoszillators 

Das Stosspendel ist dadurch gekennzeichnet, dass das rücktreibende Moment auf der einen Seite wesentlich größer ist als auf der anderen. Experimentell ergab sich für die beiden Direktionsmomente 
D₁ = 17.79 10^-3 Nm/rad und 
D₂ = 13.7 Nm/rad. 

Hier das dazugehörige Moment in Abhängigkeit von j : 

(f55) 

Hier wie im Folgenden wurde von der Funktion UnitStep[x] Gebrauch gemacht, die im MATHEMATICA-Package „DiracDelta" definiert ist. Mit ihr hat man die Möglichkeit, Sprungfunktionen und Unstetigkeiten sowie deren Ableitungen in MATHEMATICA analytisch zu behandeln. 

Man definiert die DGL des erzwungenen Stossoszillators: 

und setzt die experimentellen Werte ein: 
 

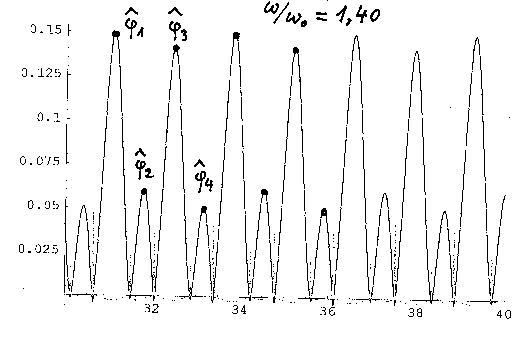
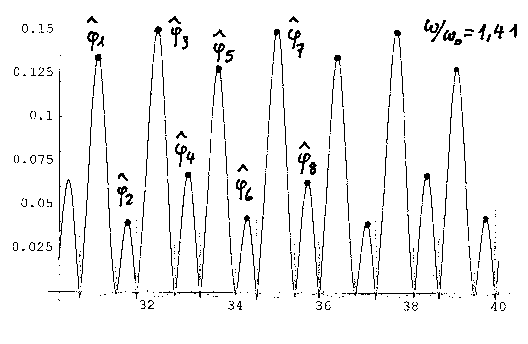
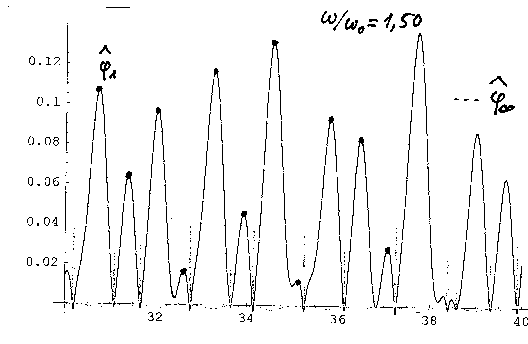
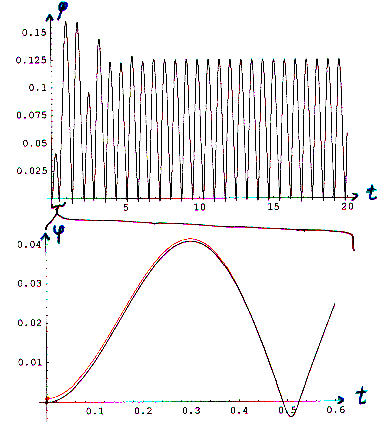
Die Ergebnisse zeigen, wie das System bei steigender Anregungsfrequenz in „klassischer" Weise über Periodenvervielfachungen ins Chaos gerät: 
 

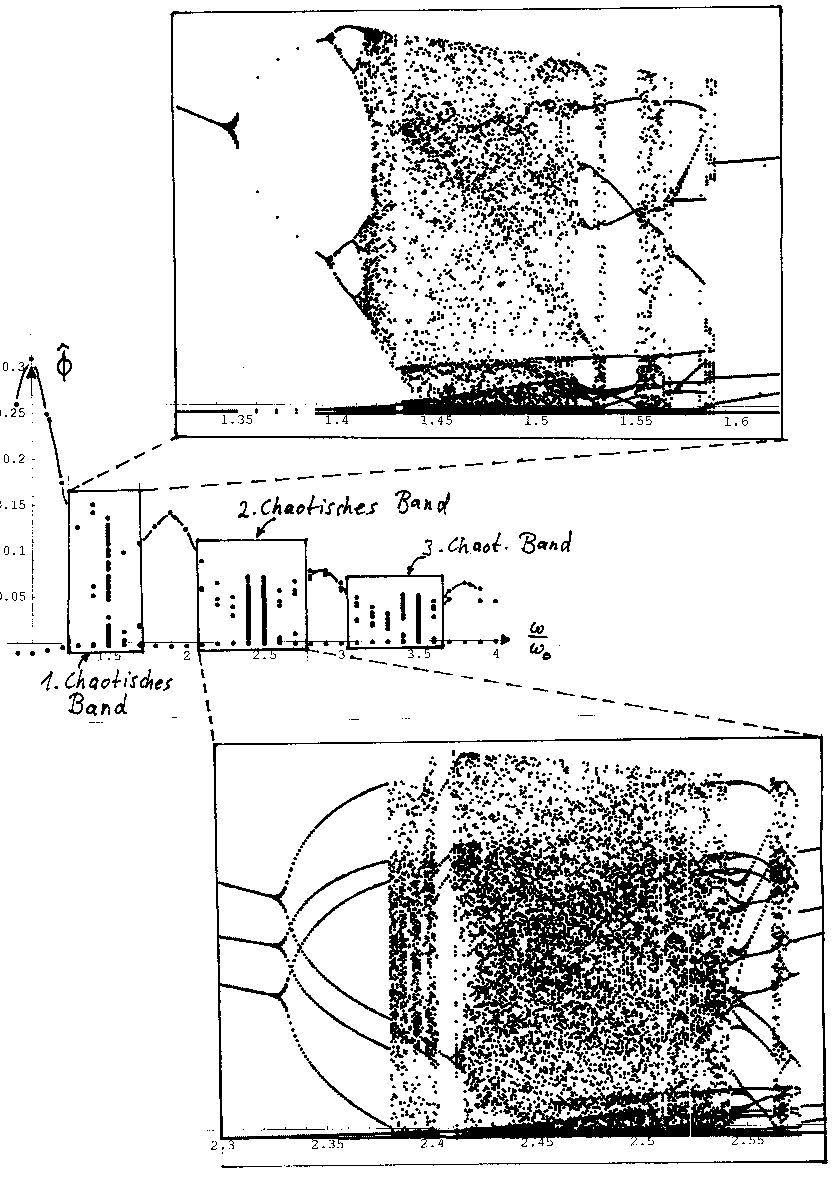
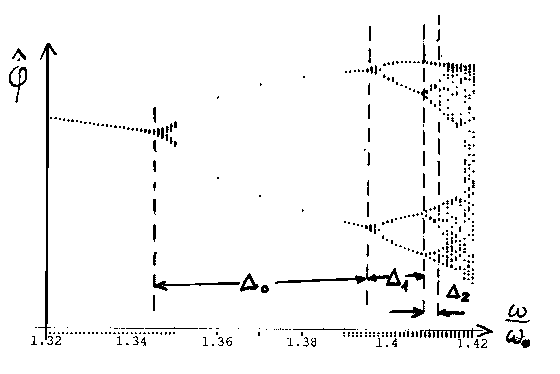
Das Bifurkationsdiagramm ( Die Scheitelwerte von  f über k = w/w₀) zeigt neben den regulären Bereichen in der Nähe der Vielfachen von w₀ eine Folge von chaotischen Bändern, die durch immer größere Komplexität gekennzeichnet sind: 

 Beim Übergang in das erste chaotische Band läßt sich auch wieder die Universalität der Feigenbaumkonstante ablesen:

  Es ergibt sich D₀ / D₁ =   3,6       und D₁ / D₂ =   3,9 .

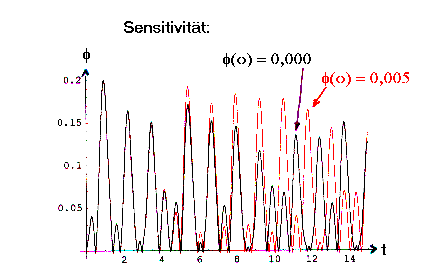
 Ebenso läßt sich die Sensibilität nachweisen, d.h. die extreme Empfindlichkeit eines chaotischen Systems für kleine Änderungen der Anfangswerte. In den folgenden Beispielen wurde das Stoßpendel für ca. 15 Sekunden  durchgerechnet, jeweils für die beiden leicht unterschiedlichen Anfangswerte f(0)= 0 und f(0)  = 0,005. 

Im chaotischen Bereich (w/w₀ =1.5) ist nach etwa 10 Sekunden keine Ähnlichkeit des Zeitverlaufs mehr erkennbar:

 Im regulären  Bereich (w/w₀ =1.3) dagegen dämpft sich die Differenz zwischen den beiden Kurven schon nach ca. 0,5 Sekunden vollständig fort:

Experimentelle Ergebnisse am Pohlschen Stossoszillator 

Neben den oben genannten kleinen Änderungen am Pohlpendel ist für das Gelingen der Experimente wichtig, die Störungen des Systems durch die Registrierung der Auslenkung möglichst gering zu halten. Ich habe die folgende sehr preiswerte opto-elektronische Methode gewählt, die sich mit Erfolg auf andere ähnliche Fälle anwenden lässt: Am inneren Kupferrad des Drehpendels wurde ein Pappsegment aufgeklebt, das bei der Bewegung eine rechteckige Blende mehr oder weniger abdeckt. 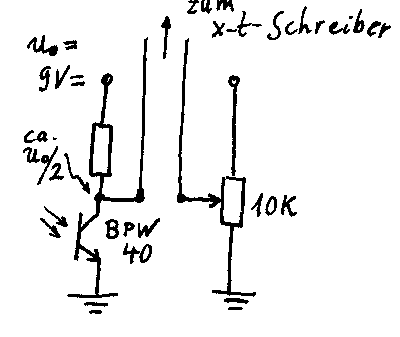Die Blende befindet sich beim Experiment zwischen einer Glühlampe und einem Projektionsobjektiv, das die Blende auf einen Phototransistor abbildet. Der Spannungsabfall am Transistor wurde in der dargestellten Weise direkt auf einen x-t-Schreiber gegeben. Die aufgezeichneten Spannungen sind bei dieser einfachen Schaltung natürlich nicht exakt proportional zur Auslenkung des Drehpendels. Das stört bei diesem Experiment aber nicht, da es hier nicht auf die exakte Bahnform ankommt, sondern im wesentlichen auf die Periode der Schwingungen. Mit geringfügig höherem elektronischem Aufwand kann man natürlich auch diese Proportionalität erreichen. 
 
 

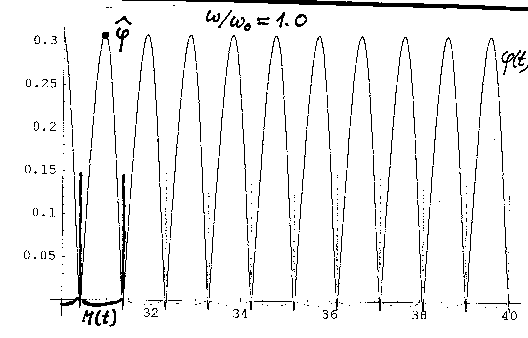
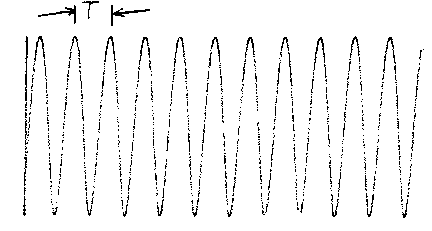
Die folgende Messreihe zeigt, wie das Pohlsche Stosspendel bei steigender Anregungsfrequenz nach dem „Feigenbaum-Szenario" über Periodenvervielfachungen ins Chaos gelangt. Die beobachteten Frequenzen stimmen dabei gut mit den Rechnungen überein. So lassen sich die Periodenverdopplung und die Periodenvervierfachung sehr reproduzierbar beobachten, was sonst nur bei wenigen mechanischen Systemen gelingt. Bei der Periodenverachtfachung ist man auch hier an der Grenze der Leistungsfähigkeit der Anordnung angelangt. Wie die Theorie zeigt, müsste man hierzu zuverlässig eine Frequenzstabilität des Antriebs von besser als 30/00 garantieren. 

w/w₀ =1.06 ;  Theorie für regulären Bereich : w/w₀ < 1.345

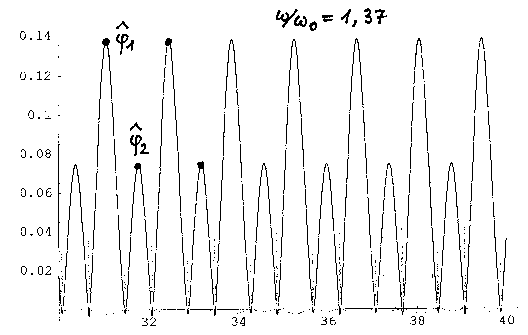
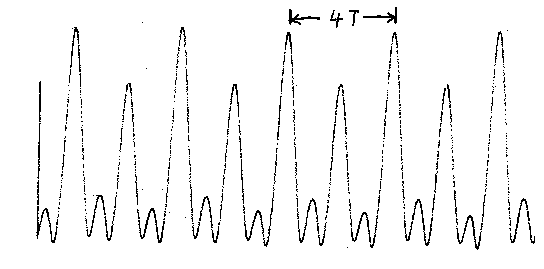
w/w₀ =1.37 ;  Theorie für Periodenverdopplung :1,345< w/w₀ < 1,395
 
 

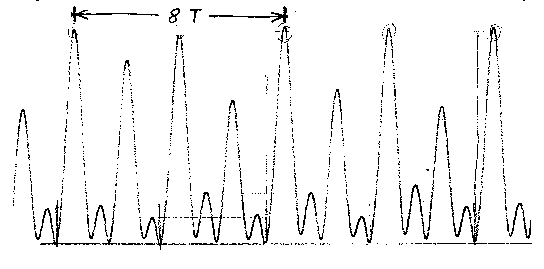
w/w₀ =1.407 ;  Theorie für Periodenvervierfachung :1,395< w/w₀ < 1,408

w/w₀ =1.42 ;  Theorie für Periodenverachtfachung: 1,408< w/w₀ < 1,412

Das Chaos selbst ist wieder sehr einfach zu beobachten, da es in einem ganzen breiten w-Bereich auftritt: 

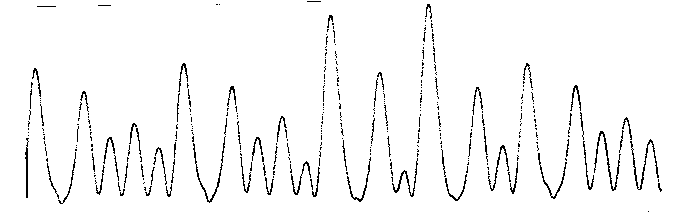
w/w₀ =1.51 ;  Theorie für das erste chaotische Band: 1,41 < w/w₀ <1.7

Leider leistet der Antrieb in der vorliegenden Form keine höheren Frequenzen, die notwendig währen, um die andere regulären Bereiche und chaotischen Bänder beobachten zu können. Wie die Rechnungen erkennen lassen, treten in diesen Bereichen potentiell sehr interessante Phänomen auf: Trifurkationen und Bistabilität, die sich dadurch zeigt, dass stabile Äste plötzlich verschwinden. Eine genauere Untersuchung dieser Phänomene wäre wahrscheinlich sehr lohnend! 

Fazit: 
Das Pohlsche Reflexpendel ist ein experimentell und theoretisch hervorragend geeignetes System, um typische Erscheinungen der nicht-linearen Dynamik zu demonstrieren. 
 
 
 

Inhalt

Die Suche nach dem "einfachsten" chaotischen System