Alle diese mechanischen Systeme eignen sich für eine quantitative Behandlung des Themas „Deterministisches Chaos" im Physikunterricht kaum, da sie sowohl experimentell als auch theoretisch zu schwierig zu handhaben sind. 
Andererseits ist bekannt, dass schon sehr einfache mathematische Modelle zur Entstehung des Chaos befähigt sind. Neben der Mandelbrot-Iteration ist die logistische Gleichung sicher das einfachste Beispiel für das chaotische Verhalten eines nicht-linearen Modells. 

Die logistische Folge („Verhulst-Dynamik") 
x_n = r x_n (1 - x_n) 
führt für r > 3.57 bekanntlich zu einem nicht-vorhersagbaren Verhalten der Folge xn : 

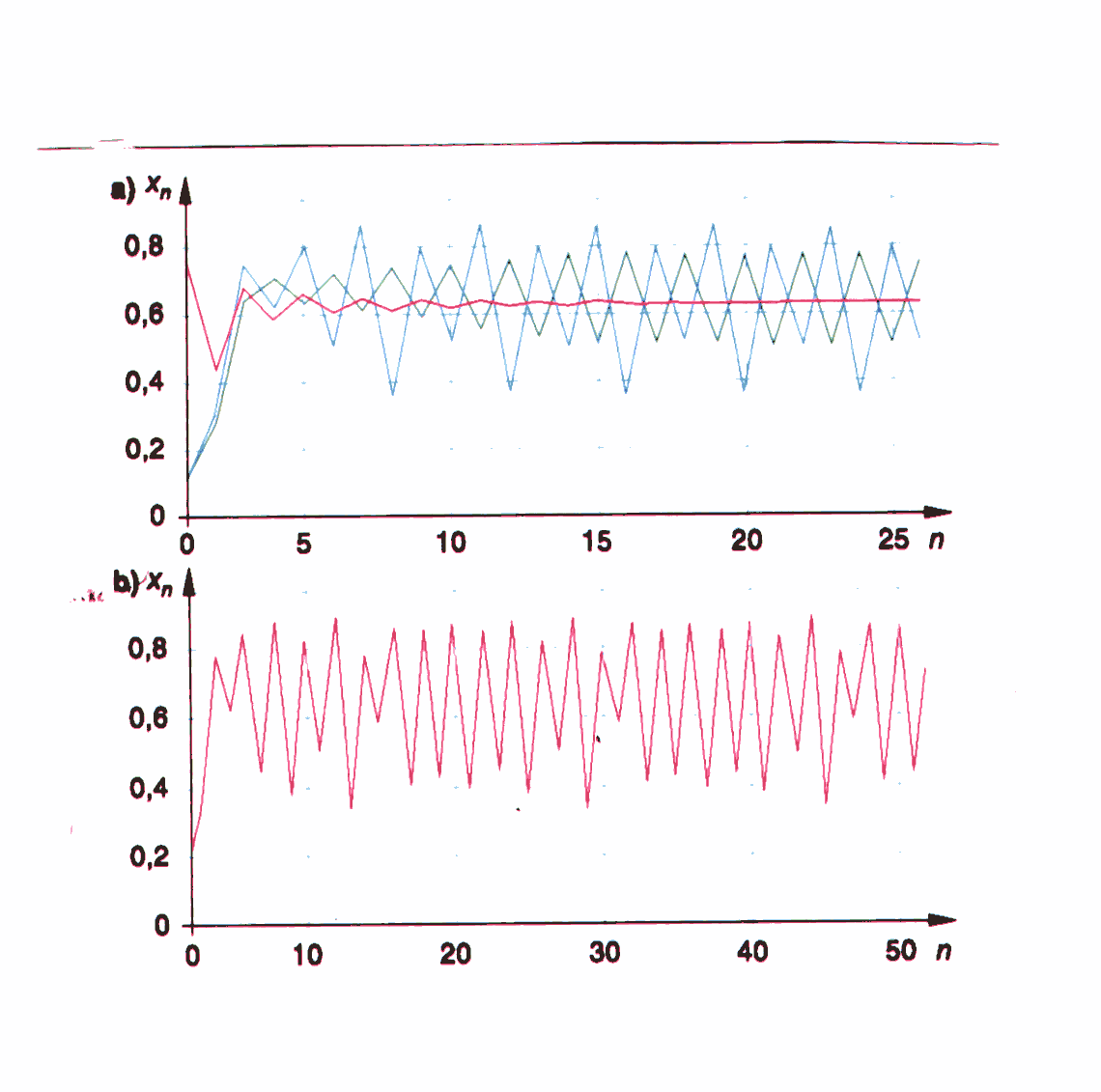
Der Übergang ins Chaos erfolgt dabei in der charakteristischen Art der „Periodenverdopplung" . Am deutlichsten lässt sich dieses Verhalten im so genannten „Bifurkationsdiagramm" beobachten. Man trägt hier über jedem r-Wert die Folge der x_n (von einem bestimmten n-Wert an, z.B. n>100) auf. 

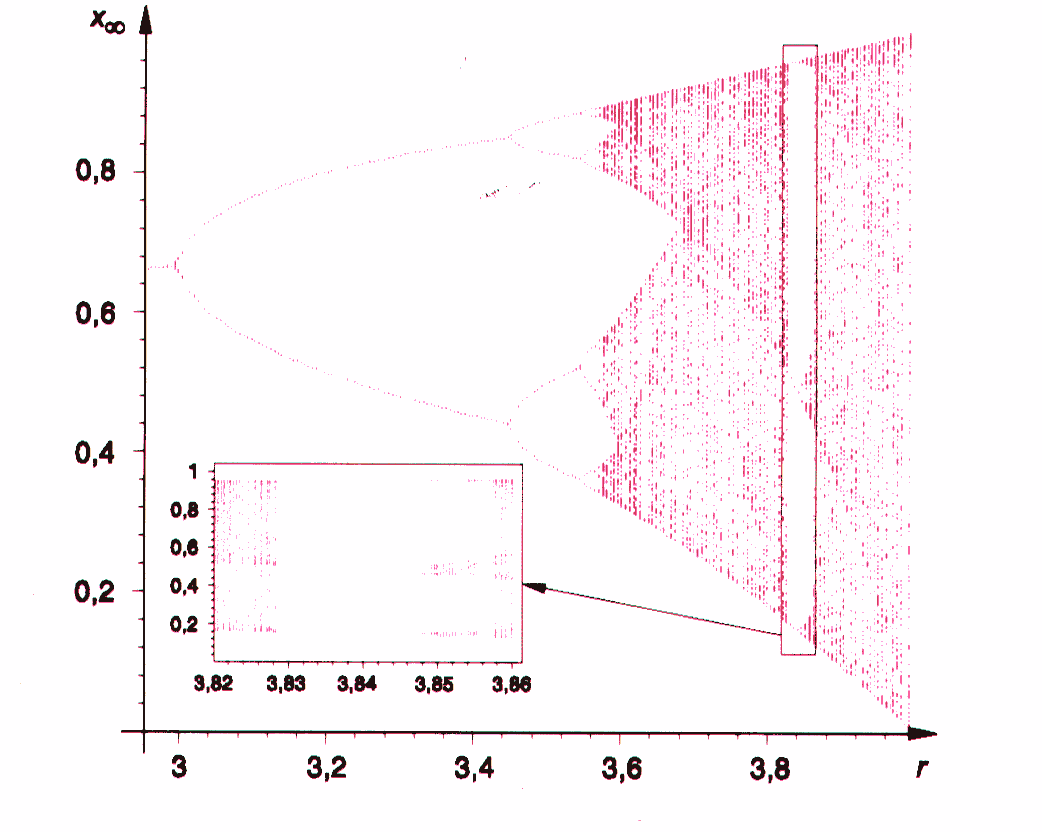
Dabei folgen die „Bifurkationspunkte" einem universellen Gesetz. Ihr Abstand wird mit wachsendem r immer kleiner. Die Abstände  D_i   zwischen aufeinander folgenden Bifurkationspunkten werden bei jeder Bifurkation etwa um einen Faktor vier kleiner. Im Grenzwert gilt das Feigenbaum-Gesetz: 

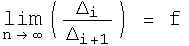
  mit einer Konstanten f („Feigenbaum-Zahl"), die für eine große Klasse von chaotischen Systemen den  universellen Wert f = 4.669.. hat. 

Lässt sich in der Physik ein ähnlich einfaches System finden? 
 
 

Das mathematische Pendel bei großem Ausschlag 

Die bisher betrachteten Systeme zeigen, dass für die Entstehung von Chaos zumindest zwei Punkte entscheidend sind: Das System muss nicht-linear sein und es sollte einen „kritischen Punkt" besitzen. Beide Bedingungen erfüllt das mathematische Pendel offensichtlich. Die dynamischen Gleichungen 

Ds / Dt = v, 
Dv / Dt = - m g sin ( s / l)
 

sind nicht-linear, und das Pendel besitzt bei s = l p einen kritischen (Überschlags-) Punkt. Betrachten wir das dynamische Vektorfeld im Phasendiagramm: 

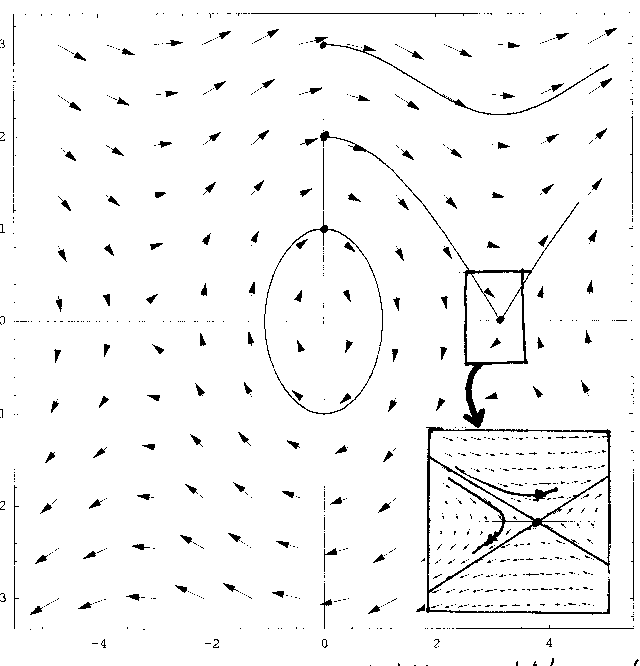
Für kleine Auslenkungen und Geschwindigkeiten ergeben sich offensichtlich geschlossene, also periodische Phasenbahnen. Der kritische Punkt (l p | 0) und zwei kritische Phasenbahnen wurden vergrößert herausgezeichnet. Man erkennt, dass das System trotz der beiden Bedingungen „Nicht-Linearität" und „kritischer Punkt" keine Neigung zum Chaos hat. 
Wie kommt das? 

Das Poincaré - Bendixson - Theorem 

Dieses Theorem besagt i.w.: 

Chaos in kontinuierlichen System ist erst ab einer Dimension von dim = 3 des Phasenraums möglich.

Kontinuierliche System sind dabei solche, bei denen die Bewegung des Phasenpunktes im Phasenraum durch eine stetige Bahn, und nicht, wie bei der logistischen Gleichung, durch eine diskrete Folge beschrieben wird. Offensichtlich können solche diskreten Systeme schon bei dim = 1 chaotisch sein. Systeme der klassischen Physik sind natürlich immer in diesem Sinne kontinuierlich. 

Was ist der anschauliche Grund für dieses Theorem? 
 

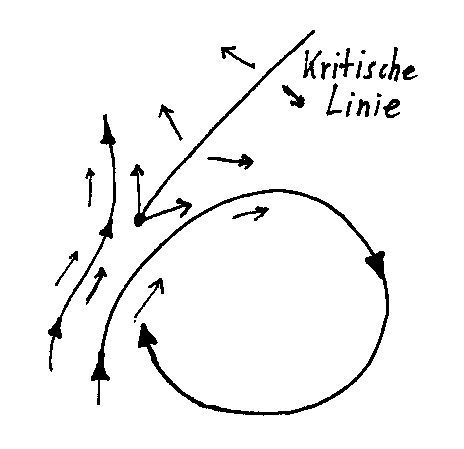Betrachten wir dazu einen 2-dimensionalen Phasenraum. Er möge, damit Chaos entstehen kann, einen kritischen Punkt besitzen. Trifft die Phasenbahn z.B. links der kritischen Linie auf, dann bewege sich das System nach links, im anderen Falle nach rechts. Chaos entsteht, wenn die Phasenbahn diesem kritischen Punkt nach einer Weile immer wieder begegnet. Sehr kleine Änderungen der Anfangsbedingungen führen in diesem Falle dazu, dass eine exakte Vorhersage darüber, welche Seite das System beim nächsten Mal passieren wird, unmöglich wird. 
Genau diese wiederholte Begegnung des Systems mit der kritischen Stelle des dynamischen Vektorfeldes sind aber im zweidimensionalen Fall unmöglich. Hat das System, wie skizziert, den rechten Weg genommen, dann müsste es, um dem kritischen Punkt ein zweites Mal zu begegnen, seine eigene Bahn überschneiden. Das ist aber auf Grund der Definition des Phasenraums ganz unmöglich, da von einem Punkt der Phasenbahn nur genau ein definierter weiterer Verlauf möglich ist. Man sieht, dass zweidimensionale Systeme sich sozusagen selbst den Weg abschneiden. Diese Beschränkung gilt ersichtlich nur für kontinuierliche Systeme, ein diskretes System, dessen „Phasenbahn" aus einzelnen Punkten besteht, kann ja über seine eigene Bahn „hüpfen". 

Der Lorenz - Attraktor 
 

Die oben angestellten Betrachtungen lassen sich gut beim Lorenz - Attraktor demonstrieren. Das DGL-System des Lorenz - Attraktors wurde 1963 von E.N. Lorenz zur Beschreibung eines meteorologischen Systems aufgestellt: 

dx/dt = a ( y - x ) 

dy/dt = b x - y - y z 

dz/dt = x y - c z

Es ist dreidimensional, nicht-linear und zeigt, wie Lorenz damals feststellte, chaotisches Verhalten. Die folgende Phasenbahn wurde für
a = 3; b = 26.5; c = 1; x(0) = z(0) = 0; y(0) =1 gerechnet. 

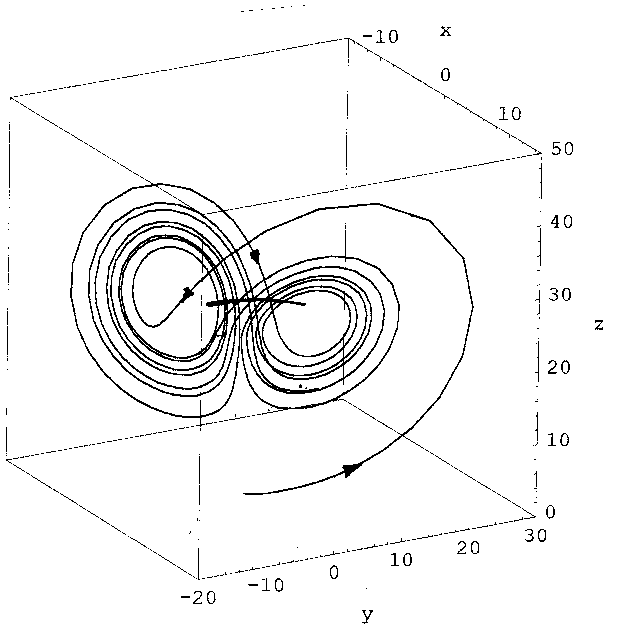
Chaos entsteht in diesem System dadurch, dass der Phasenpunkt in unvorhersagbarer Weise zwischen zwei „Scheiben" im Phasenraum hin- und herspringt. Die beiden Scheiben werden offensichtlich durch eine kritische Struktur (Linie, Ebene?) voneinander getrennt. Das System begegnet dieser Struktur immer wieder, was nur dadurch möglich ist, dass es nach dem Durchlaufen einer „Scheibe" immer wieder in die dritte Dimension ausweicht: 

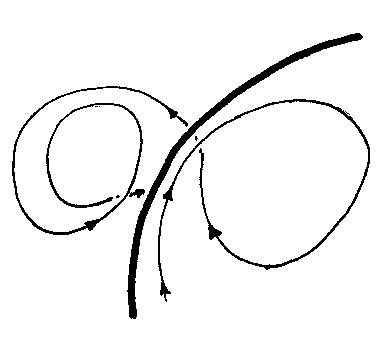
Konsequenzen für die Physik 

Wir sehen, dass das „einfachste" chaotische System einen dreidimensionale Phasenraum haben muss. Das Pendel erfüllte diese Bedingung nicht. 
Man kann nun einen weiteren Freiheitsgrad einführen. Man gelangt so z.B. zum Doppelpendel, das sich eindeutig chaotisch verhält. Die Einführung eines solchen zusätzlichen Freiheitsgrades erhöht aber die Dimension des Phasenraums um 2, da für jeden Freiheitsgrad die Angabe von Orts- und Impulskoordinate notwendig ist. Das „Tassenproblem" zeigt uns die Lösung: Man kann als zusätzliche Dimension die Zeit verwenden. Im Falle eines mechanischen Systems kann das am einfachsten durch eine äußere Kraft geschehen. Die einfachsten chaotischen Systeme werden demnach eindimensionale Systeme mit Antrieb sein. Die erwünschte Beschränktheit des Phasenraums führt dann folgerichtig zu einer 

Inhalt

Chaotische Systeme

Ein neues Schulexperiment zum Chaos