Differentialgleichungen
höherer, insbesondere 2. Ordnung
Um die beschriebene Methode auf mechanische Probleme anwenden zu können,
muss man mit ihr die Newtonsche Gleichung, also ein DGL 2.Ordnung, lösen
können. Hierzu sollte man sich zunächst an den grundlegenden
mathematischen Satz über DGLen höherer Ordnung erinnern:
Jede DGL n-ter Ordnung
y(n) = f ( y(n-1) , y(n-2) , ... y',
x, t )
lässt sich durch die Einführung der neuen Funktionen
y1 = y, y2 = y', ... yn = y(n-1)
in ein System von DGLen 1.Ordnung umformen:
y1' = y2,
y2' = y3,
.
.
yn-1 ' = yn,
yn' = f (yn, y n-1,...y3,y2,y1,x,t).
Man beachte, dass es sich bei diesem Satz nicht um etwas tiefliegend
Mathematisches, sondern um eine reine Umbenennung von Funktionen handelt:
Die Ableitungen bekommen einfach neue Namen! Das ist für uns nichts
Neues, denn die erste Ableitung s'(t) nennen wir ja schon v(t). Der obige
Satz bedeutet also für die Lösung der Newtonschen Gleichung:
Die DGL 2.Ordnung m s''(t) = F (s,s',t) ("Newtonsche Gleichung") lässt
sich durch die Einführung der neuen Funktion v = s'(t) in zwei DGLen
1.Ordnung umwandeln, nämlich:
s'(t) = v(t)
m v'(t) = F(s(t),v(t),t) .
Die erste Gleichung ist also nur die Definition der Geschwindigkeit
und die zweite Gleichung enthält die Dynamik.
Schreiben wir beide Gleichungen für endliche Schrittweite um, so
ergibt sich:
Ds = v Dt,
Dv = f(s,v,t) Dt
.
Zur Lösung eines solchen Gleichungssystems gehen wir wieder in
einem (s|v)- Koordinatensystem von einem Anfangszustand (s0|v0)
zur Zeit t0 aus und berechnen mit Hilfe der beiden Gleichungen
den nächsten Punkt (s1|v1) zur Zeit t1.
Das Verfahren soll an zwei einfachen System demonstriert werden:
Gleichförmig beschleunigte Bewegung
Da die Ergebnisse für diesen Fall als bekannt vorausgesetzt werden,
kann die Behandlung zur Überprüfung des Verfahrens dienen.
Das DGL-System lautet hier:
Ds / Dt = v, Dv
/ D t = konstant
Das Pfeildiagramm wird mit den MATHEMATICA-Befehlen

erstellt:
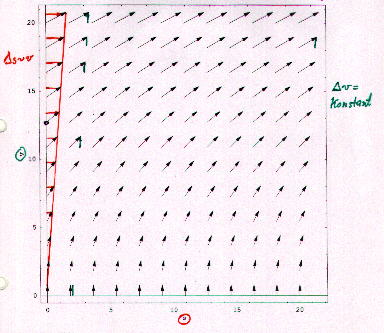
Die Pfeile haben also wie angedeutet eine konstante v-Komponente und
eine s-Komponente ~ v. Die Lösungen des DGL-Systems sind die Parabelscharen
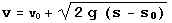 ,
die sich aus ,
die sich aus 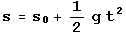 und und 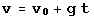 ergeben. ergeben.
Die Parabeln reichen für großes t beliebige Werte von s und
v.
Dies ist im folgenden Beispiel anders:
Freier Fall mit Luftwiderstand
Der Luftwiderstand kann im einfachsten Fall (turbulente Strömung)
durch eine der Bewegung entgegengesetzte Beschleunigung ~ v2
beschrieben werden:
Ds / Dt = v,
Dv / Dt = g -
c v2 .
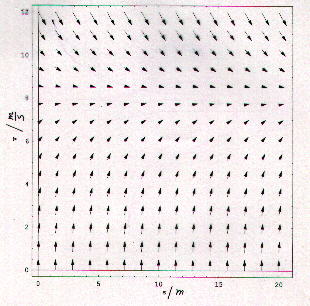
Während die s-Komponente der Pfeile wieder konstant ist, nimmt
die v-Komponente positive oder negative Werte an, je nachdem v kleiner
oder größer als (g/c)1/2 ist. Die Lösungskurven
nähern sich folglich ganz unabhängig von den Anfangswerten der
Geraden
v = (g/c)1/2 an. Diese Gerade ist ein Beispiel für
ein Gebilde, das wir weiter unten einen „Attraktor" nennen werden und das
bei den chaotischen Systemen eine wichtige Rolle spielt.
 Inhalt Inhalt
 Eine
zeitabhängige Differentialgleichung 1. Ordnung Eine
zeitabhängige Differentialgleichung 1. Ordnung
 Phasenraum
und Phasenbahn Phasenraum
und Phasenbahn
|