Im nächsten Beispiel geht es um eine explizite Zeitabhängigkeit. Das Lutschproblem war in dem Sinne zeitunabhängig als das Pfeilsystem nur von m abhing: Die Pfeile auf Parallelen zur m-Achse waren daher überall gleich. Betrachten wir nun das "Kaffeetassenproblem":
Eine Flüssigkeit mit Anfangstemperatur T₀ soll sich durch Wärmeleitung der Umgebungstemperatur T_A angleichen, wobei T_A selbst zeitlich veränderlich ist. In unserem Beispiel steigt T_A exponentiell von T₁ = 200K auf T₂ = 300K an:    T_A (t) = T₂  -( T₂ -T₁) e^{-l t}. 
 

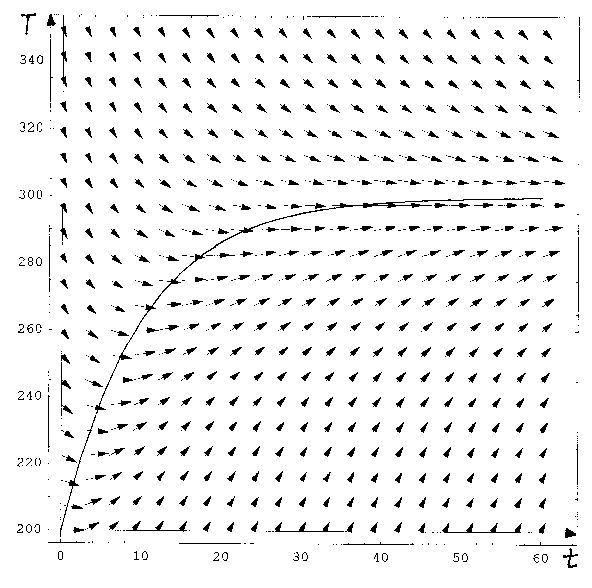
Für die zeitliche Änderung von T ergibt sich daher der Ansatz DT = a ( T_A(t)  -T(t) )Dt. Wie im vorigen Beispiel zeichnen wir auch hier wieder die Pfeile im T-t-System: 

Dieses Mal hängen diese Pfeile nicht nur von T sondern auch von t ab: Die Pfeile zeigen immer in Richtung auf die Kurve  T_A(t) (durchgezogene Linie). Die gleiche grafische Methode wie vorhin liefert Lösungen T(t), die alle bei T(t) =  T_A(t) ein Minimum haben. Dort zeigen die Pfeile ja horizontal. Mit etwa mehr Aufwand ist auch hier eine exakte Lösung  zu finden. Es handelt sich um eine lineare inhomogene DGL. Sie hat die Lösung 

 T(t)  =   a  (T₁- T₂)/(a- l) (e^{-l t} -e^-at) +  e^-at  (T₀- T₂) + T₂) . 

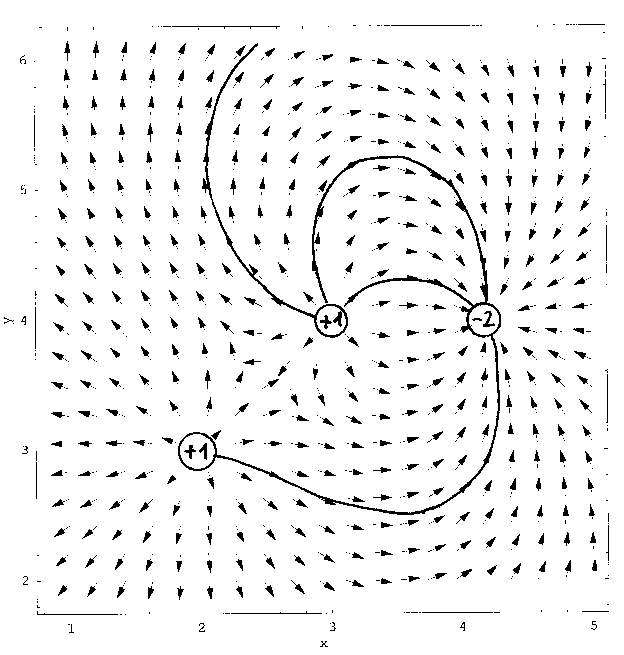
Die benutzte grafische Methode sollte in den Grundzügen schon in der SI einmal aufgetaucht sein, nämlich bei der Behandlung von Feldlinien. Sie ergeben sich aus dem elektrischen oder magnetischen Kraftfeld genauso wie die Lösungen der DGL aus dem Pfeilsystem. Ein System von Magnetnadeln oder, wie im folgenden Beispiel, ein System von elektrischen Kraftpfeilen kann ganz konkret als Wegweiser im Raum aufgefasst werden. Startet man an einem beliebigen Punkt des Feldes und folgt den Pfeilen, dann beschreibt man eine einzelne Feldlinie: 

Die Pfeilsysteme der vorangegangenen Beispiele wurden mit MATHEMATICA berechnet. MATHEMATICA ist das z.Zt. wohl mächtigste Computeralgebrasystem für den PC. Für den Unterricht empfiehlt es sich vor allem durch folgende Eigenschaften: 

- Es ist interaktiv. Jede Zeile wird nach Art eines Interpreters an den "Kernel", das eigentliche Verarbeitungsprogramm, übergeben und abgearbeitet. Die Wirkungen von Änderungen des Codes können daher sofort beobachtet werden. 

- MATHEMATICA verfügt über bestechende Grafikmöglichkeiten. 

- Programmcode kann in den meisten Fällen in der gewohnten mathematischen Schreibweise eingegeben werden. 

- Das Programm ist durch Preissenkungen in den vergangenen Jahren sehr erschwinglich geworden. 

Trotzdem lassen sich mit MATHEMATICA auch umfangreiche Programme schreiben. Als Nachteil könnte man anführen, dass die von MATHEMATICA verwendete Programmiermethode (funktional statt prozedural) zu Beginn einige Schwierigkeiten mit sich bringt, insbesondere für den Benutzer, der eine prozedurale Sprache wie PASCAL gewohnt ist. 

Für das Zeichnen von Vektorfeldern gibt es in MATHEMATICA einen eigenen Befehl (PlotVectorField). Das obige E-Feld wurde so durch die folgenden wenigen Programmzeilen erzeugt: 

Inhalt

DGLen höherer Ordnung