Chaotische Systeme sind dadurch charakterisiert, dass sich ihr zeitliches Verhalten langfristig nicht vorhersagen lässt. 

Die Tatsache, dass streng deterministische System unvorhersagbares Verhalten zeigen, ist erstaunlich und wurde lange Zeit "verdrängt".

- Wie kommt dieses Verhalten zustande? 
- Was unterscheidet ein chaotisches System von einem regulären? 

Legen wir unsere Vorstellung vom Phasenraum und seiner Dynamik zugrunde, dann ist die Frage:
 
 

Wie kann man sich in einem Raum verirren, wo an jedem Punkt ein Wegweiser steht? Eine Lösung zeigt dieses  Bild, bei dem der Wanderer an einem "kritischen" Punkt ankommt und sich nur mit Hilfe des berühmten Schmetterlings für den weiteren Weg entscheiden kann.
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

Beispiele für chaotische mechanische Systeme finden sich in großer Zahl: 

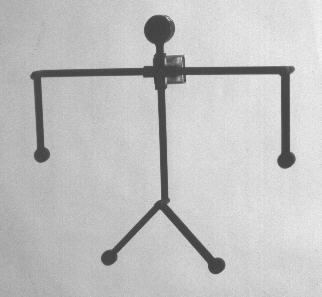
Meist sind es Systeme mit einer großen Zahl von Freiheitsgraden, die  einen oder mehrere "kritische Punkte" besitzen, d.h. Bahnpunkte, die zwei grundsätzlich verschiedene Bewegungsformen voneinander trennen. 

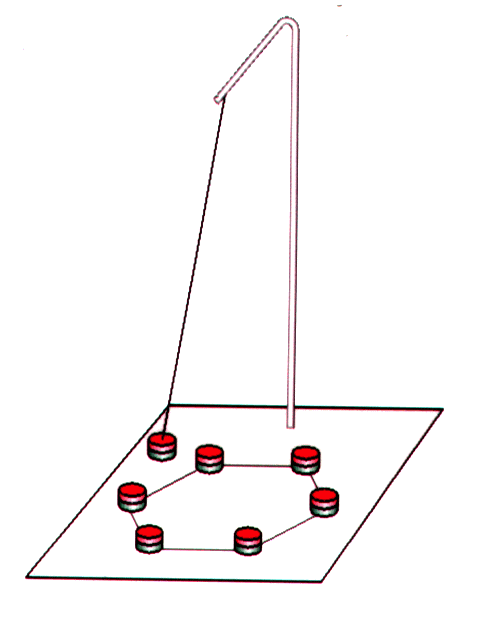Ein relativ einfaches System ist das Magnetpendel. Ein ebenes Pendel, das aus einem Faden mit angehängtem Magneten besteht, lässt man über einer Anordnung von mehreren anziehenden Magneten pendeln. Es beschreibt komplizierte Bahnen, bis es schließlich bei einem bestimmten Magneten zur Ruhe kommt. Da das System durch die Bewegungsgleichungen streng determiniert ist, kann auch die Endposition nur von den Anfangsbedingungen abhängen. Andererseits erkennt man aber auch, dass die Endposition sehr empfindlich auf kleine Änderungen der Anfangsbedingungen reagieren wird. Wie die meisten chaotischen Systeme hat auch dieses kritische Punkte, die Linien nämlich, die genau zwischen zwei Magneten liegen. 
 
 
 
 
 
 

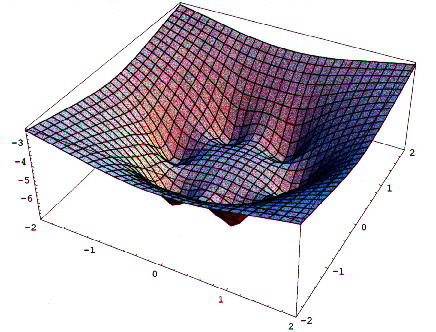
Im Potentialverlauf sind dies die Sattelflächen zwischen zwei Magneten (hier für sechs Magnete dargestellt): 

Die experimentelle Untersuchung des Systems ist eine langwierige und mühevolle Aufgabe. Man lässt das Pendel dazu an einem bestimmten Punkt (x0,y0) aus der Ruhe los und beobachtet, an welchem der Magnete das Pendel zur Ruhe kommt. Man markiert diesen Startpunkt dann mit der "Farbe" dieses Magneten und erhält so die "Einzugsgebiete" der Magnete. 
 
 
 
 
 
 
 
 
 

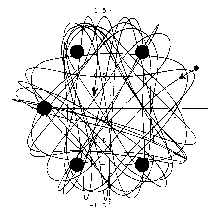Leichter lässt sich das Ergebnis durch Berechnung bestimmen. Für sechs Magnete ergibt sich ohne Reibung eine endlose nichtperiodische Bahnkurve:
 
 
 
 
 
 
 
 
 
 
 

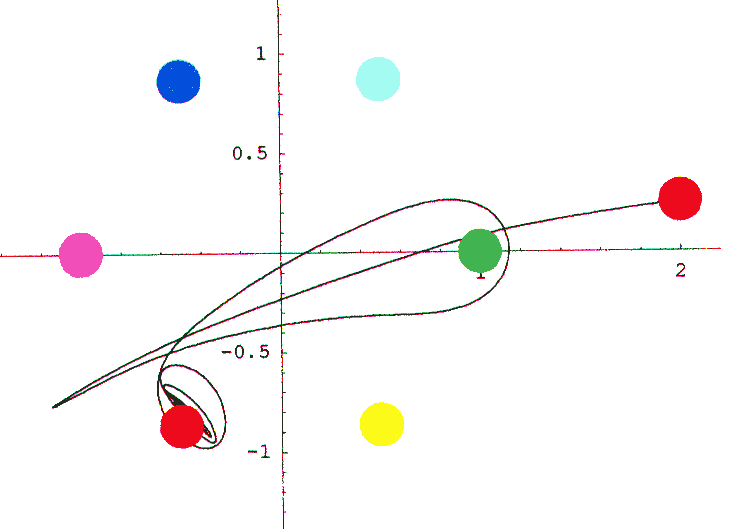Mit Reibung endet die Bahn immer an einem bestimmten Magneten, hier z.B. an dem "roten", entsprechend wird der Startpunkt rot markiert:
 
 
 
 
 
 
 
 
 
 

Markiert man so einen ganzen Bereich, ergibt sich  für 3 Magnete: 

und  für sechs Magnete: 

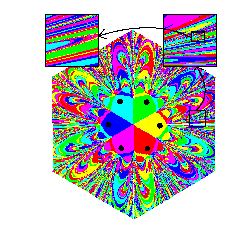
Es ergibt sich die für chaotische System charakteristische "fraktale" Struktur. Während die Einzugsgebiete in der Nähe der Magnete zusammenhängend sind, sind sie weiter außen in jeder beliebigen Vergrößerung betrachtet unendlich fein miteinander gemischt. 
 
 
 

Inhalt

Phasenraum und Phasenbahn 

Die Suche nach dem "einfachsten" chaotischen System