Phasenraum und
Phasenbahn
Wir haben hier den Zustand eines mechanisches System mit einem Freiheitsgrad
(s) durch einen Punkt P(s(t)|v(t)) in der s-v-Ebene charakterisiert. Die
Angabe eines solchen Zustands bestimmt aber nicht nur den Zustand selber,
sondern über die dynamischen Gleichungen auch sein weiteres (und auch
bisheriges) zeitliches Verhalten. Die Menge aller Punkte P(s(t)|v(t)) bezeichnet
man als Phasenraum und die Linie, die P auf Grund bestimmter Anfangswerte
durchläuft, als Phasenbahn. Der Wert dieser Begriffsbildung
liegt u.a. darin, dass die Phasenbahn das u.U. komplexe Verhalten eines
physikalischen Systems geometrisch anschaulich macht.
Das soll im folgenden Beispiel gezeigt werden. Außerdem werden
wir die vorgestellte Methode hierbei zum ersten Mals dazu benutzen,
ein neues Ergebnis herzuleiten.
Der harmonische Oszillator
Eine rücktreibende Kraft proportional zur Auslenkung führt
bekanntlich auf die DGL des harmonischen Oszillators.
Wie auch in den vorhergegangenen Beispielen lässt sich das Verfahren
gut mit Übungsblättern und parallel dazu mit Folien in einem
Kurs erarbeiten. Nach Aufstellung des DGL-Systems
D s / D t = v,
D v / D t = -
w02
s = - D/m s .
wird nunmehr das Pfeilsystem Schritt für Schritt konstruiert.
Die dynamischen Gleichungen besagen, dass D
s ~ v (horizontale Pfeile) und D v ~ - s ist
(vertikale Pfeile). Da weder Ds von s noch Dv
von v abhängt, sind die s-Komponenten auf horizontalen Linien und
die v-Komponenten auf vertikalen Linien konstant. Man erhält daher
das folgende Bild:
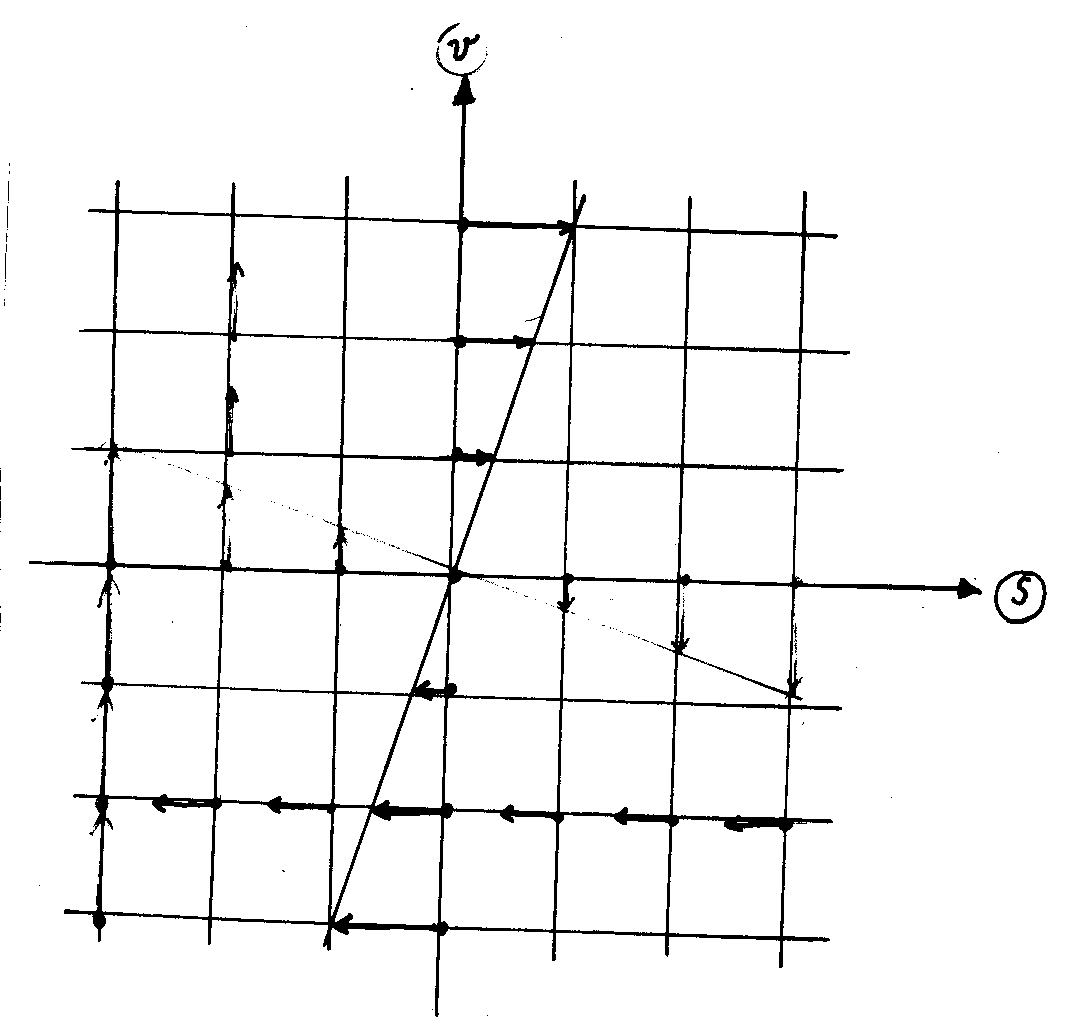
Vervollständigt man das Pfeilsystem und konstruiert man die resultierenden
Pfeile (Vektorsummen der Komponenten), dann wird die Struktur des Vektorfeldes
klar:
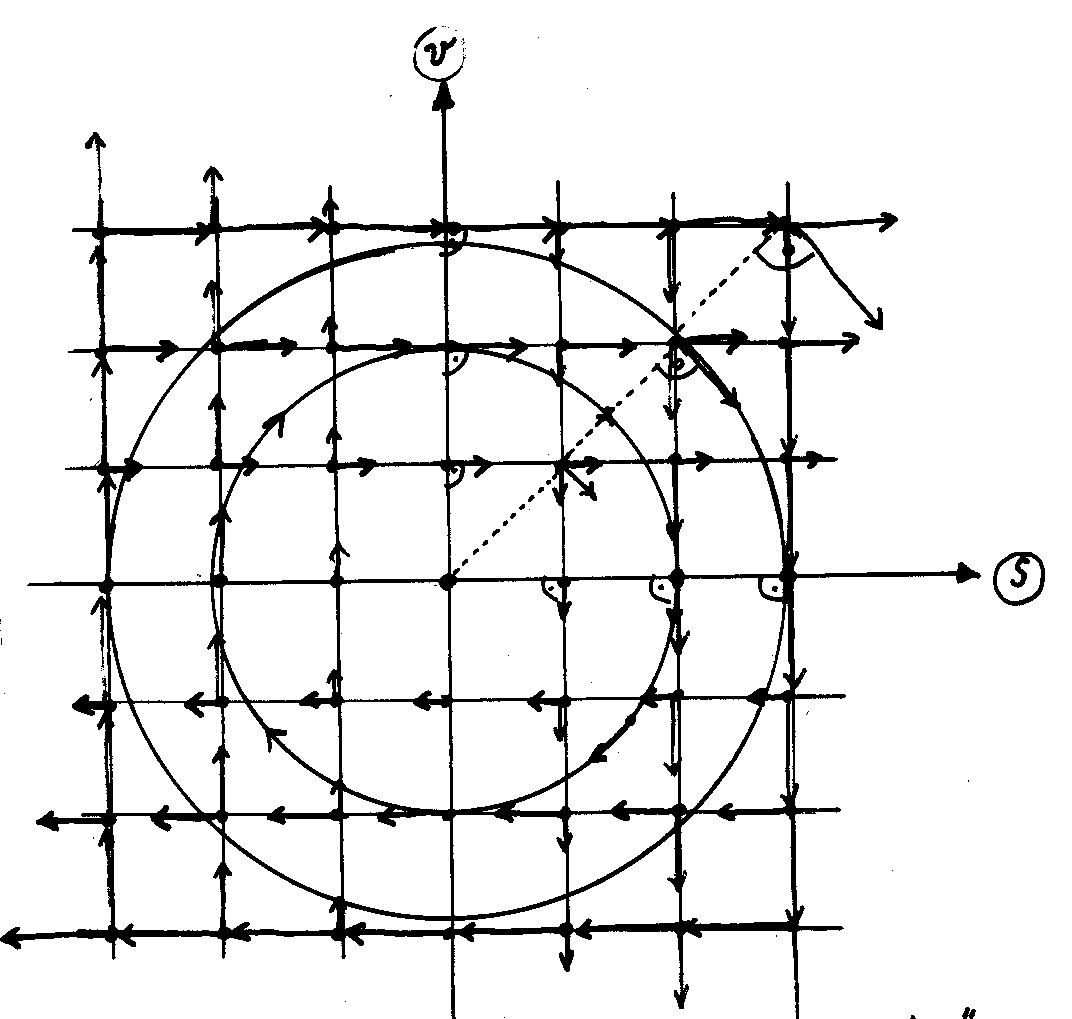
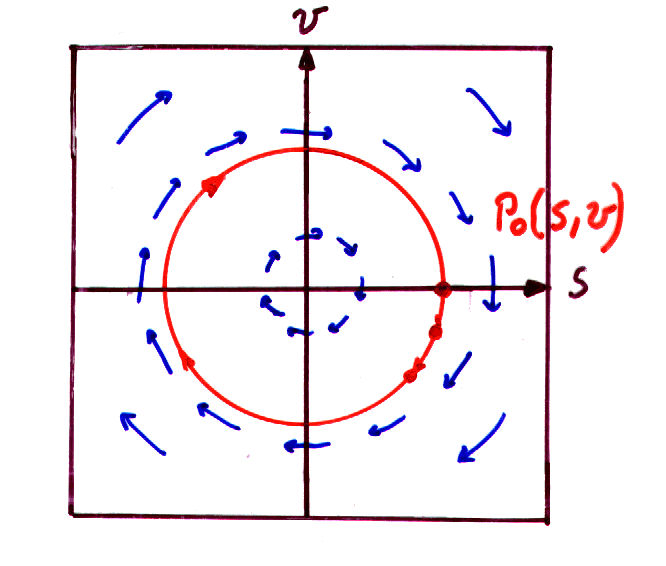
Die dynamischen Pfeile stehen überall senkrecht auf dem Radius,
sie bilden also ein Wirbelfeld. Startet man die Bewegung mit einer beliebigen
Anfangsbedingung, also an einer beliebigen Stelle der s-v-Ebene, so beschreibt
das System eine geschlossene Bahn. Wählt man die Einheiten des s-v-Systems
so, dass die Scheitelwerte 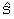 und und 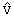 gleich groß sind, dann ist die Bahn ein Kreis. Streng genommen trägt
man also nicht s und v auf, sondern s/
gleich groß sind, dann ist die Bahn ein Kreis. Streng genommen trägt
man also nicht s und v auf, sondern s/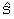 und v/
und v/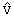 und die Phasenbahnen sind Einheitskreise. Da die Pfeile bei gleichem Radius
auch gleich lang sind, ist die Bahngeschwindigkeit auf den Phasenbahnen
konstant, die Phasenpunkte machen also eine gleichförmige Kreisbewegung
mit der Winkelgeschwindigkeit w . Daraus ergeben
sich sofort die s(t) und v(t) -Funktionen:
und die Phasenbahnen sind Einheitskreise. Da die Pfeile bei gleichem Radius
auch gleich lang sind, ist die Bahngeschwindigkeit auf den Phasenbahnen
konstant, die Phasenpunkte machen also eine gleichförmige Kreisbewegung
mit der Winkelgeschwindigkeit w . Daraus ergeben
sich sofort die s(t) und v(t) -Funktionen:
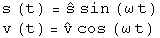
Betrachtet man die dynamischen Vektorpfeile, dann sieht man, dass sie
nach außen proportional zum Radius länger werden. Da der Umfang
der Phasenbahnen ebenfalls proportional zum Radius wächst, ist die
Umlaufzeit für alle Phasenbahnen gleich groß. Die Frequenz des
harmonischen Oszillators ist also unabhängig von der Amplitude.
Der Wert der Winkelgeschwindigkeit w ergibt
sich aus folgender Überlegung: Betrachtet man die Bewegung des Phasenpunktes
bei s=0 und v=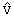 ,
dann hat sein Geschwindigkeitspfeil dort wegen der oben beschriebenen Normierung
die Länge Ds/ ,
dann hat sein Geschwindigkeitspfeil dort wegen der oben beschriebenen Normierung
die Länge Ds/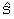 . Die Winkelgeschwindigkeit des Phasenpunktes ist also
. Die Winkelgeschwindigkeit des Phasenpunktes ist also
w = Df/Dt = Ds/(1 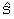 Dt)
= Dt)
= 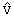 Dt/( Dt/(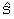 Dt)= Dt)=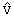 / /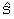 . .
An der Stelle v=0 und s = 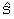 ergibt sich andererseits für dieselbe Winkelgeschwindigkeit
ergibt sich andererseits für dieselbe Winkelgeschwindigkeit
w = - Dv /(1 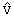 Dt)
= w02 Dt)
= w02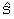 Dt/(
Dt/(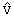 Dt)
= w02 Dt)
= w02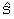 / /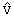 =w02
/ w. Bei der Umwandlung wurde die dynamische
Gleichung benutzt. Also folgt w = w0. =w02
/ w. Bei der Umwandlung wurde die dynamische
Gleichung benutzt. Also folgt w = w0.
Man sollte anmerken, dass diese wichtigen Ergebnisse über den harmonischen
Oszillator ganz ohne Analysis gewonnen wurden. Insbesondere wurden dabei
weder Kenntnisse über die Ableitungen der trigonometrischen Funktionen
noch die Kettenregel benötigt.
Die gedämpfte Schwingung
Beim gedämpften Oszillator tritt eine zusätzliche rücktreibende
Kraft proportional zur Geschwindigkeit hinzu:
Ds / Dt = v,
Dv / Dt = - w02s
- l v.
Dadurch bekommen alle dynamischen Pfeile eine zusätzliche Komponente
in Richtung auf die s-Achse:
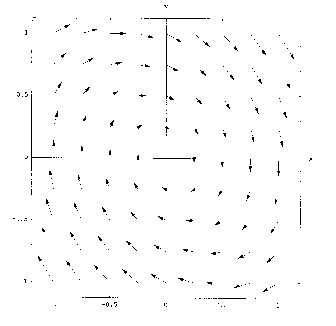
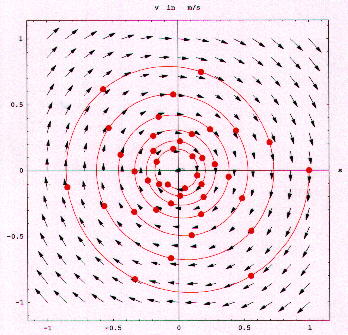
Das Vektorfeld ist ein nach innen gerichteter "Strudel". Alle Phasenbahnen
werden daher nach innen gezogen. Es entstehen Spiralen, die schließlich,
unabhängig vom Startpunkt, alle im Ursprung enden. Im folgenden Plot
wurden die Phasenpunkte in gleichen zeitlichen Abständen gezeichnet.
Die Dimension des Phasenraums
Um den Zustand eines Systems (und sein weiteres zeitliches Verhalten)
vollständig zu beschreiben, benötigten wir beim "Bonbonproblem"
nur eine einzige Angabe, nämlich die Masse. Sein Phasenraum ist also
eindimensional:

Beim "Tassenproblem" und beim den bisher behandelten einfachen mechanischen
Systemen sind es zwei Angaben (Temperatur und Zeit bzw. Ort und Geschwindigkeit).
Der zugehörige Phasenraum ist also zweidimensional:
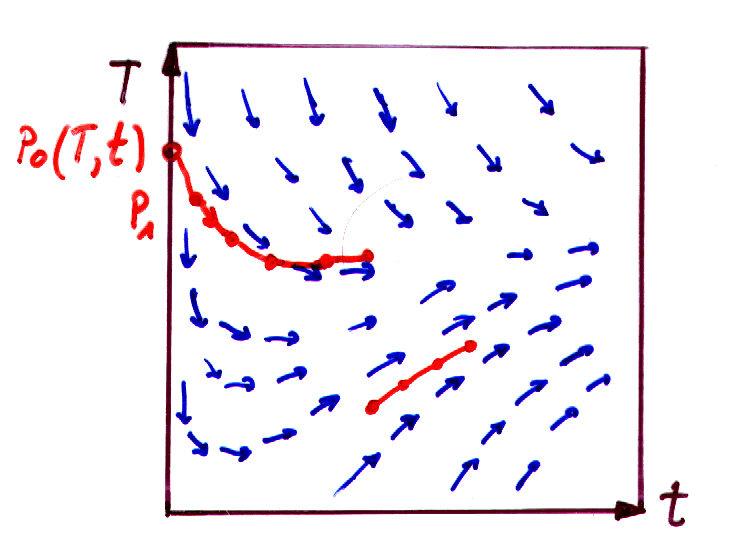 
Der Grund dafür ist folgender: Die DGL des "Tassenproblems" ist
1.Ordnung aber zeitabhängig während die DGL der betrachteten
mechanischen Problemen selbst schon von 2.Ordnung ist. In beiden Fällen
lässt sich die Dynamik anschaulich durch ein System von Wegweisern
in der Ebene darstellen und die DGL in der vorgeführten Art grafisch
lösen.
Die Phasenbahnen zeigen auch das Langzeitverhalten eines Systems. Während
nicht-periodische Systeme offene Bahnen beschreiben, sind periodische Systeme
durch eine geschlossene Phasenbahn charakterisiert. Manche Bahnen nähern
sich im Laufe der Zeit asymptotisch einer Kurve oder einem Punkt an ("Attraktor")
oder sie verharren schon von Beginn an auf derselben Bahn.
 Inhalt Inhalt
 Differentialgleichungen
2. Ordnung Differentialgleichungen
2. Ordnung
 Chaotische
Systeme Chaotische
Systeme
|