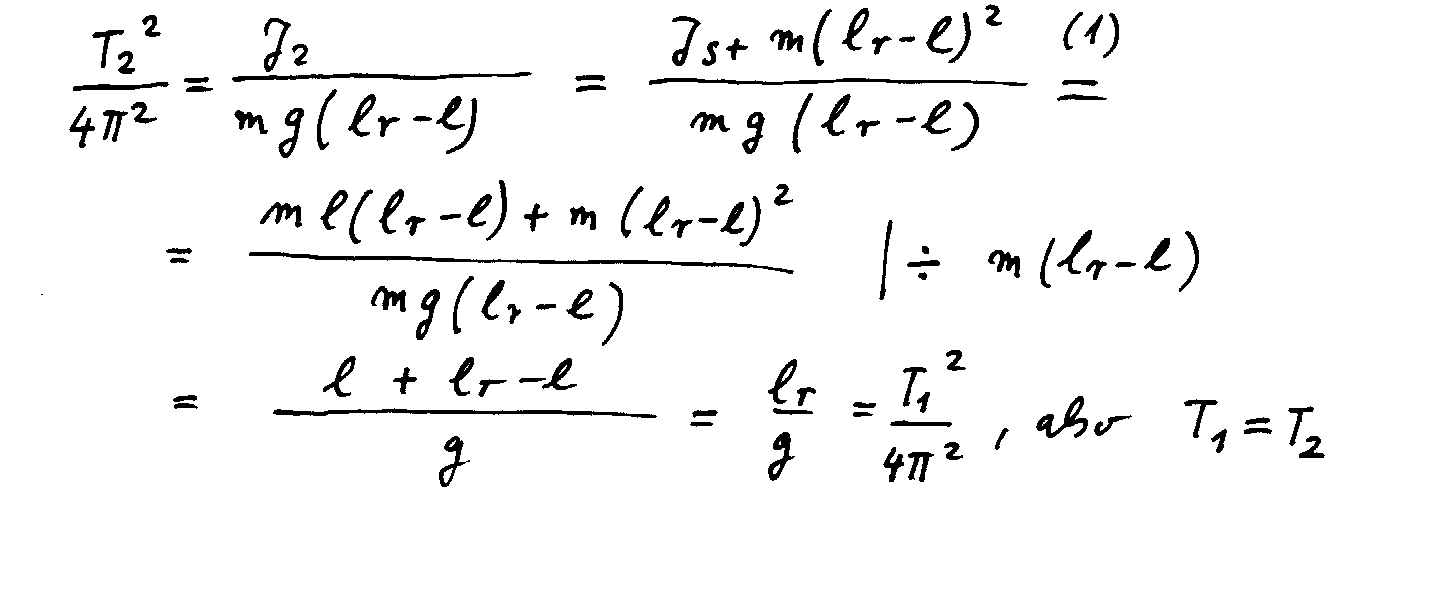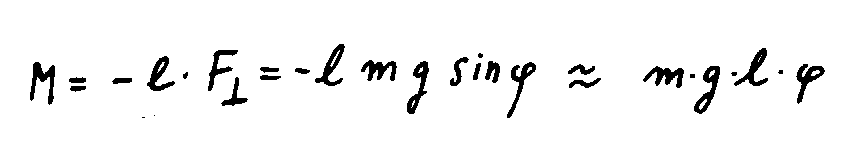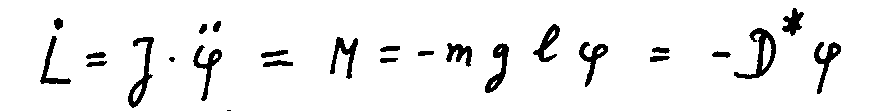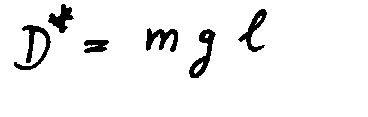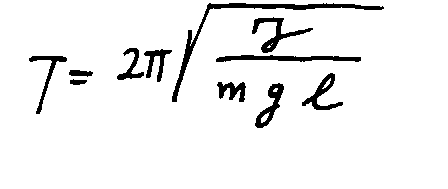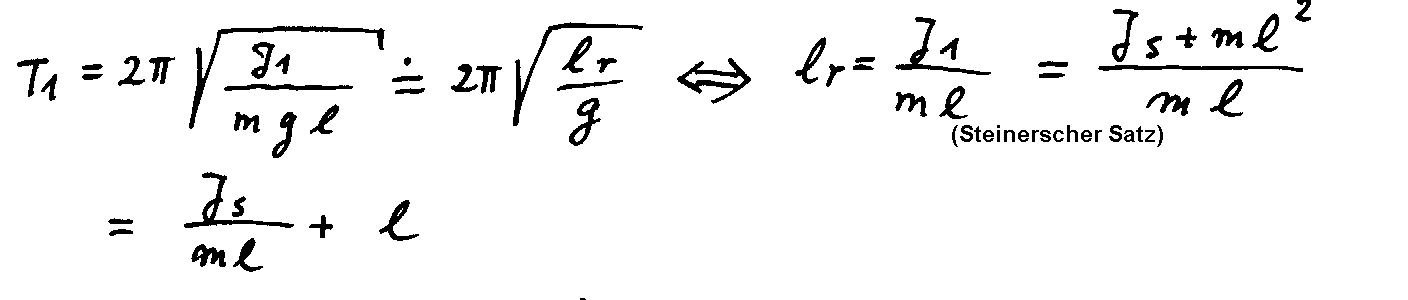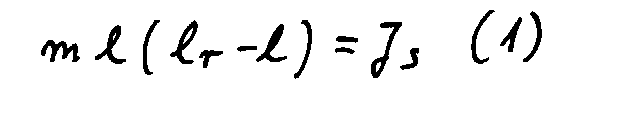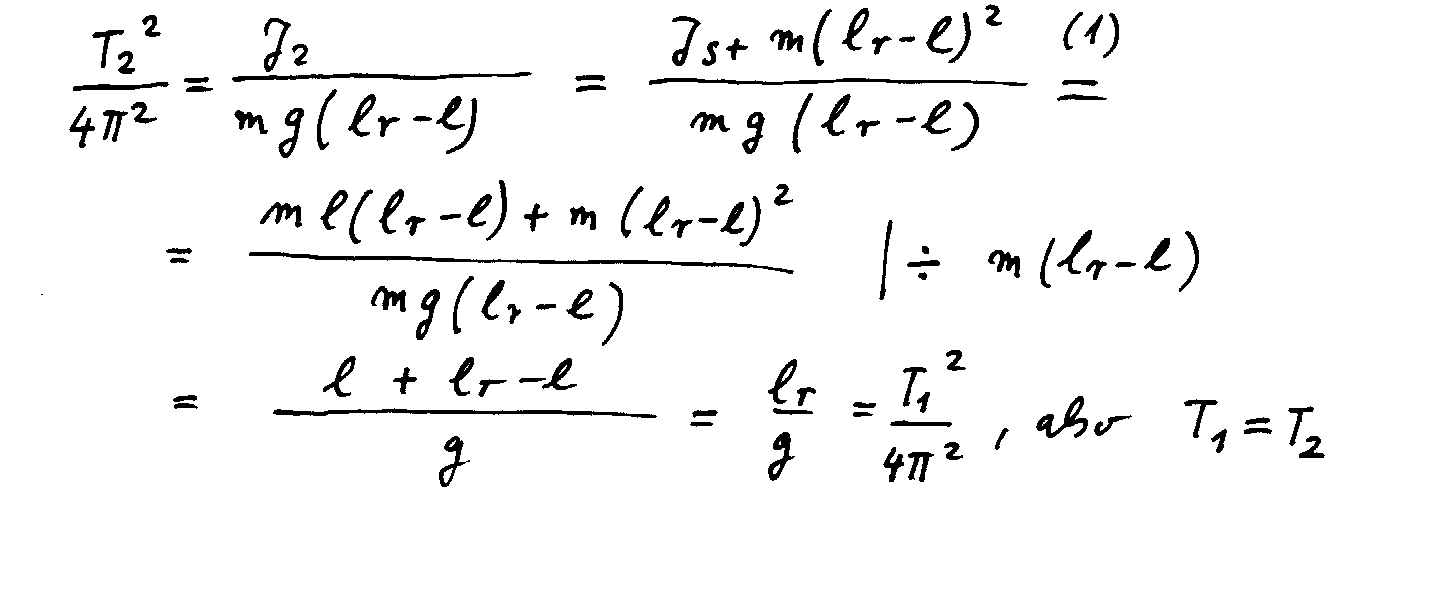Das Reversionspendel –
eine Präzisionsmessung der Erdbeschleunigung mit
einfachsten Mitteln
von:
Dr. Joachim Bolz
Paul-Klee-Gymnasium
51491 Overath
Die Bestimmung der Erdbeschleunigung mit dem Reversionspendel
ist eine klassische Methode, die mit einfachsten experimentellen Mitteln
als Praktikumsversuch durchgeführt werden kann und dabei bei einiger
Sorgfalt g-Werte mit besser als ..... Promille Genauigkeit liefert. Dazu
ist die Diskussion und Berücksichtigung der verschiedenen Fehlerquellen
erforderlich, worin u.a. der Reiz dieses Experiments liegt. Die erreichbare
Genauigkeit ist groß genug, um die Ortsabhängigkeit von g eindeutig
nachzuweisen und eignet sich daher auch für ein Projekt, an dem sich
mehrere Arbeitsgruppen aus unterschiedlichen Gegenden Deutschlands beteiligen
könnten.
Im Prinzip eignet sich die Messung von Schwingungsdauer
und Länge eines mathematischen Pendels wegen T = ..... zur Bestimmung
von g. Das Problem besteht dabei in der genauen Messung von l, dem
Abstand des wahren Drehpunkts des Pendels vom Schwerpunkt der möglichst
punktförmigen Masse. Eine genaue Bestimmung von T erfordert ein Pendel,
das lange ohne Antrieb schwingt, also eine möglichst große Masse
hat, was sich wiederum schwer mit der Punktförmigkeit der Masse in
Einklang bringen lässt.
Das Reversionspendel vermeidet diese Schwierigkeit
Es handelt es sich dabei um ein physikalisches Pendel, das um zwei
unterschiedliche Drehpunkte schwingen kann. Neben der Schwingungsdauer
muss nur der exakte Abstand dieser beiden Drehpunkte gemessen werden,
was wesentlich einfacher und genauer möglich ist als die Messung des
Schwerpunkts einer ausgedehnten schwingenden Masse.
Die Schwingungsdauer des physikalischen Pendels ist 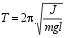 ,
wobei J das Trägheitsmoment des Pendels um den Drehpunkt D und l der
Abstand zwischen Drehpunkt und Schwerpunkt S ist (-> Anhang 1). Als „reduzierte
Länge“ lr eines solchen Pendels bezeichnet man die Länge
eines mathematischen Pendels mit gleicher Schwingungsdauer, als „Schwingungsmittelpunkt“
Sm denjenigen Punkt auf der Verbindungslinie D–S, der
von D den Abstand lr hat. Es zeigt sich, dass sich die Schwingungdauer
eines physikalischen Pendels nicht ändert, wenn man den Drehpunkt
in den Schwingungmittelpunkt verlegt, das Pendel also umkehrt und um den
Schwingungmittelpunkt schwingen läßt („Reversion“ = Umkehrung,
-> Anhang 2). Hat man also die beiden Punkte D1 und D2
gefunden, die bei ein und demselben Pendel gleiche Schwingungsdauern T1
= T2 = T liefern, dann ist deren Abstand lr, und die Erdbeschleunigung
lässt sich mit der Formel
,
wobei J das Trägheitsmoment des Pendels um den Drehpunkt D und l der
Abstand zwischen Drehpunkt und Schwerpunkt S ist (-> Anhang 1). Als „reduzierte
Länge“ lr eines solchen Pendels bezeichnet man die Länge
eines mathematischen Pendels mit gleicher Schwingungsdauer, als „Schwingungsmittelpunkt“
Sm denjenigen Punkt auf der Verbindungslinie D–S, der
von D den Abstand lr hat. Es zeigt sich, dass sich die Schwingungdauer
eines physikalischen Pendels nicht ändert, wenn man den Drehpunkt
in den Schwingungmittelpunkt verlegt, das Pendel also umkehrt und um den
Schwingungmittelpunkt schwingen läßt („Reversion“ = Umkehrung,
-> Anhang 2). Hat man also die beiden Punkte D1 und D2
gefunden, die bei ein und demselben Pendel gleiche Schwingungsdauern T1
= T2 = T liefern, dann ist deren Abstand lr, und die Erdbeschleunigung
lässt sich mit der Formel 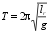 bestimmen. Statt bei festem Pendel die Drehpunkte zu verändern, hält
man besser die Drehpunkte fest und verändert den Schwerpunkt des Pendels
durch Verschieben eines Gewichts. Hierzu genügen auch endlich viele
Positionen des Gewichts, die so gewählt werden, dass beim Verschieben
zwischen den äußersten Lagen des Gewichts die beiden Schwingungsdauern
T1 und T2 um die Drehpunkte D1 bzw.
D2 ihre Größen von T1 < T2
nach T1 > T2 ändern.
bestimmen. Statt bei festem Pendel die Drehpunkte zu verändern, hält
man besser die Drehpunkte fest und verändert den Schwerpunkt des Pendels
durch Verschieben eines Gewichts. Hierzu genügen auch endlich viele
Positionen des Gewichts, die so gewählt werden, dass beim Verschieben
zwischen den äußersten Lagen des Gewichts die beiden Schwingungsdauern
T1 und T2 um die Drehpunkte D1 bzw.
D2 ihre Größen von T1 < T2
nach T1 > T2 ändern.
Bei dem von uns verwendeten Pendel (s. Skizze)
ist das der Fall.
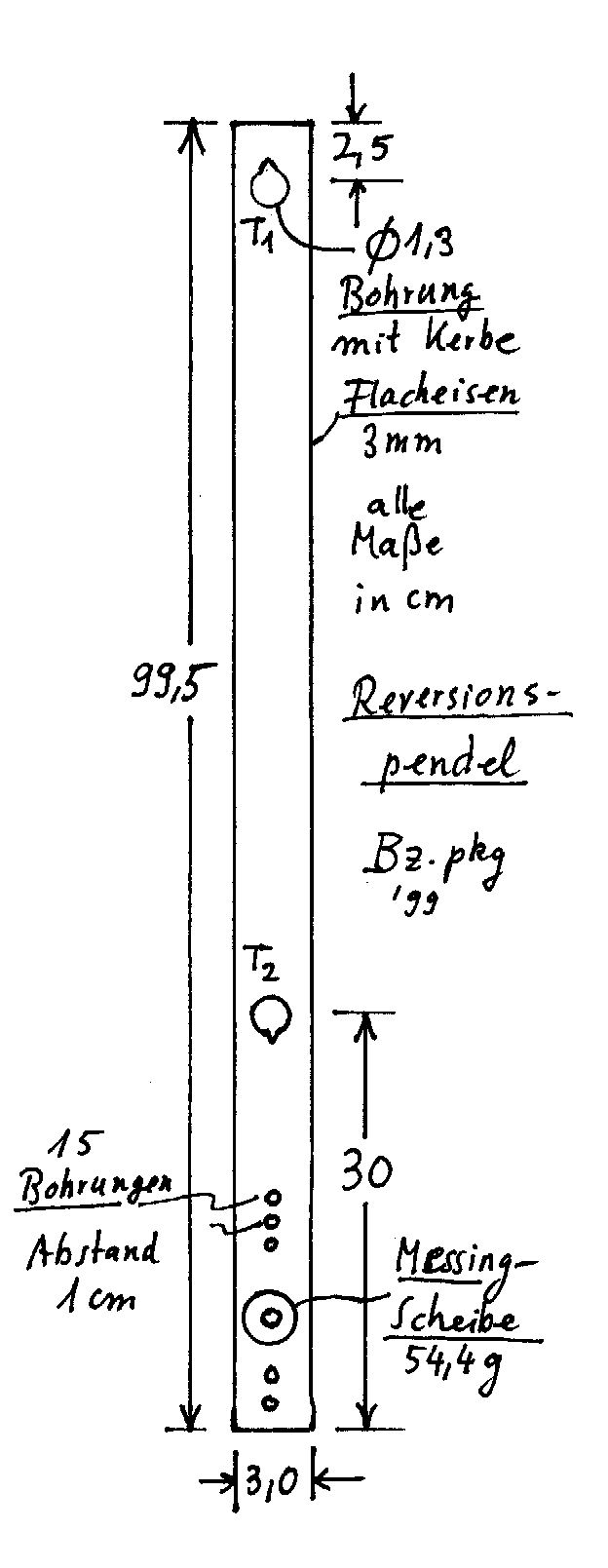
Als Schneide wird eine Rasierklinge verwendet, die in
die gesägte Kerbe eines kurzen Messingstabes eingeklebt wurde:

Bei der Messung wird das Pendel vorsichtig auf die Schneide
gesetzt und dann für alle Positionen des Gewichts die beiden Schwingungsdauern
bestimmt.



Zur Bestimmung von T = T1 = T2 trägt
man T1 und T2 gegen die Position p des Gewichtes
auf und bestimmt den Schnittpunkt (p,T) der beiden Geraden T1(p)
und T2(p). T ist dann die gesuchte Schwingungsdauer.
Ziel des hier beschriebenen Experiments soll eine mit
dem vorliegenden Pendel möglichst genaue Bestimmung von g sein. Bevor
man das Experiment durchführt, muss man sich daher überlegen,
mit welcher Genauigkeit die Größen ls und T bestimmt werden
müssen, da beide zum Fehler von g beitragen. Während die Genauigkeit
von T durch Erhöhung der Messzeit leicht erhöht werden kann,
ist ls die Größe, die die Genauigkeit des Endergebnisses bestimmt.
Zunächst wird daher der Abstand der beiden Kerben, um die das Pendel
im Betrieb schwingt, möglichst genau gemessen. Zur Messung wird ein
gutes Edelstahl-Bandmass und eine Lupe zum Ablesen verwendet. Vorsicht!
Einfache Bandmaße aus dem Baumarkt zeigen bis zu 1mm Unterschied
bei einer Messlänge von einigen Metern. Das ist für dieses Experiment
nicht tolerierbar. Das Bandmass wird bei jeder Messung neu auf das Pendel
gelegt und mit Klebeband fixiert. Vorsichtshalber wird auch die Temperatur
bestimmt, bei der die Messung stattfand, da in diesem Stadium noch nicht
klar ist, ob möglicherweise die Temperaturausdehnung des Pendels berücksichtigt
werden muss. Man liest jeweils neu die Lage der linken und der rechten
Kerbe ab. Bei einer Messreihe ergaben sich so folgende Werte:
| linke Kerbe [cm] |
rechte Kerbe [cm] |
ls [cm] |
| 104,48 |
40,04 |
68,44 |
| 105,08 |
36,64 |
68,44 |
| 113,26 |
44,84 |
68,42 |
| 118,32 |
44,84 |
68,42 |
| 124,35 |
55,93 |
68,42 |
| 143,02 |
74,60 |
68,42 |
| 138,24 |
69,80 |
68,44 |
| 132,56 |
64,12 |
68,44 |
| 117,45 |
49,02 |
68,43 |
| 120,52 |
52,09 |
68,43 |
Daraus folgt: ls = (68,430 ± 0,003)
cm.
Mit dieser relativ primitiven Methode läßt
sich also ls mit einer Genauigkeit von 0,04 Promille
bestimmen. Da wegen g = .....
die Zeit T doppelt gewichtet in das Endergebnis eingeht, muss T auf ca.
0,02 0/00 = 2×10-5 genau bestimmt werden, um einen ebenso
großen Betrag zum Fehler des Endergebnisses zu liefern wie
ls. Eine einfache Stoppuhrmessung hat eine Genauigkeit von.
dt ~ 0.1s. Für die Zahl N der gemessenen Schwingungen muss also gelten:
dt /( N T ) <= 2×10-5, N×T
>= 0.1s / 2×10-5 = 5000s ~ 1.4 h. Es ist klar, dass das
verwendete Pendel so lange ohne Antrieb nicht mit ausreichender Ampli-tude
schwingt. Eine Messung zeigt folgendes Dämpfungsverhalten:
a) Position T1 (Gewicht unten)
| N T /s |
Amplitude am Pendelende in cm |
|
|
|
|
|
|
b) Position T2 (Gewicht oben)
| N T /s |
Amplitude am Pendelende in cm |
|
|
|
|
|
|
Man muss also eine genauere Zeitmessung wählen. Verwendet
man eine Lichtschranke, dann wird dt ~ 0.001 s und man kommt mit ca. 50s
~ ..... T Gesamtmesszeit aus.
In der folgenden Messreihe wurden daher etwa ..... Schwingungen
..... mal ausgemessen:
Anhang
1) Schwingungsdauer des physikalischen Pendels
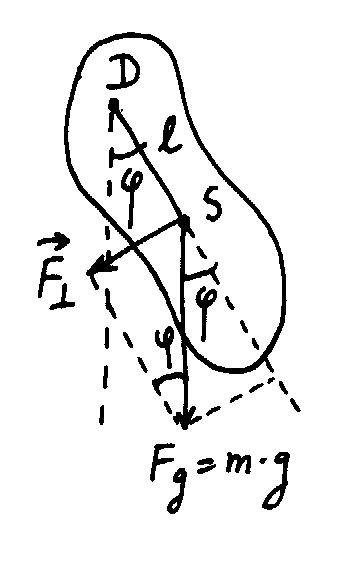
Das (rücktreibende) Drehmoment ist
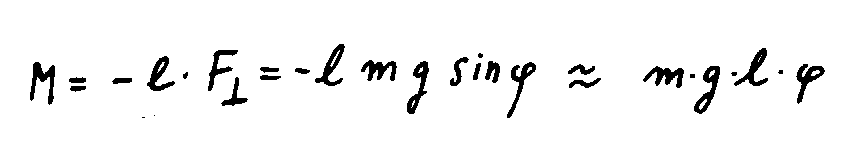
eingesetzt in die Bewegungsgleichung
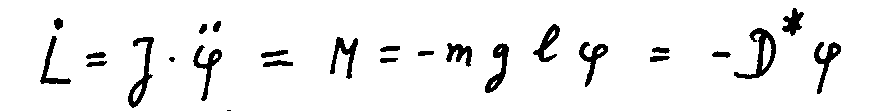
mit
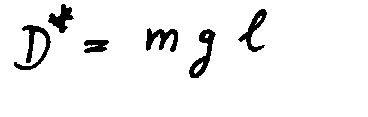
ergibt sich eine harmonische Schwingung

also
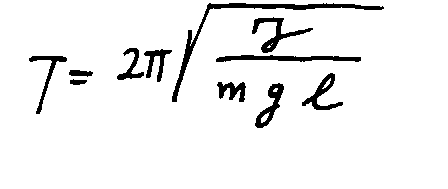
2) Reversion und reduzierte Pendellänge
Im Folgenden ist J1,2 = Trägheitsmoment
des Pendels um D1 bzw. D2, JS = Trägheitsmoment
des Pendels um den Schwerpunkt S.
Die reduzierte Pendellänge lr ist
definiert durch
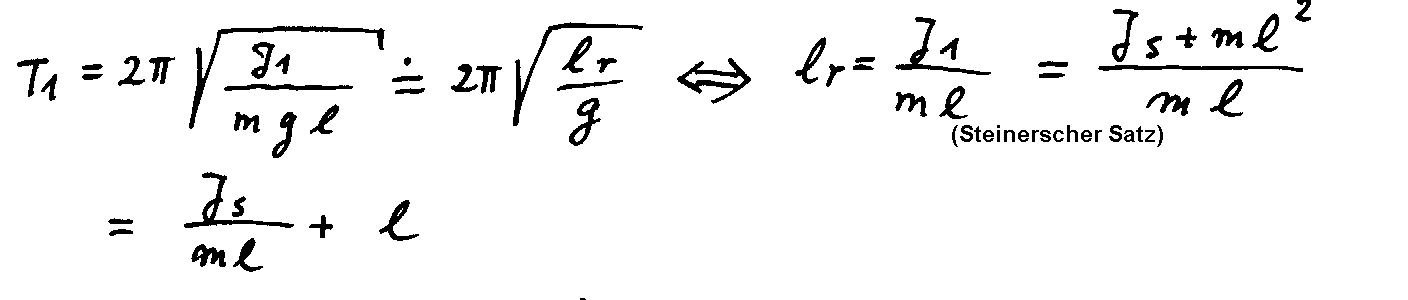
also
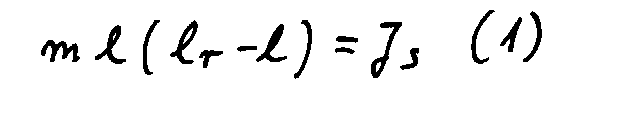
Für die Schwingungsdauer T2 um D2
gilt