
GPS-Satelliten: Bahnen
von
Dr. Joachim Bolz
Paul-Klee-Gymnasium
51491 Overath
Seit 1993 kreisen 24 Satelliten in etwa 20000 km Höhe um die Erde und bilden zusammen mit Bodenstationen das erdumspannende Navigationssystem GPS, das nicht nur Flugzeugen und Schiffen zur Verfügung steht, sondern inzwischen auch in Kraftfahrzeugen und von Wanderern, Bergsteigern, Jägern usw. genutzt wird.

GPS-Satelliten: Bahnen
Jeweils vier Satelliten haben eine gemeinsame Umlaufbahn, so dass es insgesamt sechs Umlaufbahnen gibt. Die Bahnen sind alle um 55° gegenüber dem Äquator geneigt und um jeweils 60° längs des Äquators gegeneinander versetzt.
Die Anordnung der Bahnen ist so gewählt, dass die Satelliten ihre Bahnspuren auf der Erdoberfläche etwa alle 24 Stunden (4 Minuten früher pro Tag) wiederholen.
An Bord eines jeden Satelliten befinden sich drei hoch präzise Atomuhren, deren Synchronisation ständig per Funk überwacht wird. Die Hauptkontrollstation des Systems befindet sich bei der Schriever Air Force Base (früher Falcon AFB) in Colorado. Die weltweit verteilten Kontrollstationen messen die Zeitsignale der Satelliten, in der Hauptkontrollstation werden daraus die exakten Bahnen und die notwendigen Zeitkorrekturen für jeden Satellit berechnet und hochgeladen. Alle 24 Satelliten senden nach jeweils einer Millisekunde codierte Funksignale auf der Frequenz 1,6 GHz (19 cm Wellenlänge), die neben der Kennung des jeweiligen Satelliten die aktuellen Bahnparameter und die exakte Zeit der Signalaussendung enthalten.
Beispiel für einen Datensatz:
GPS Satellite Ephemeris and Clock Parameters
Gathered 4/18/95 21:36:00
Austron 2201A GPS Satellite Receiver
EPHEMERIS FOR SATELLITE 2 :
PRN number for data .................. 2
Issue of ephemeris data .............. 224
Semi-Major Axis (meters) ............. 2.65603E+07
C(ic) (rad) .......................... 1.88127E-07
C(is) (rad) .......................... -1.00583E-07
C(rc) (meters) ....................... 321.656
C(rs) (meters) ....................... 87.6875
C(uc) (rad) .......................... 4.36418E-06
C(us) (rad) .......................... 2.70829E-06
Mean motion difference (rad/sec) ..... 5.04521E-09
Eccentricity (dimensionless) ......... 0.0139305
Rate of inclination angle (rad/sec) .. 4.11089E-10
Inclination angle @ ref. time (rad) .. 0.950462
Mean Anomaly at reference time (rad) . -2.62555
Corrected Mean Motion (rad/sec) ...... 0.000145859
Computed Mean Motion (rad/sec) ....... 0.000145854
Argument of perigee (rad) ............ -2.56865
Rate of right ascension (rad/sec) .... -8.43857E-09
Right ascension @ ref time (rad) ..... 1.75048
Sqrt (1 - e^2) ....................... 0.999903
Sqr root semi-major axis, (m^1/2) .... 5153.67
Reference time ephemeris (sec) ....... 240704
Der Empfang so schwacher Signale ist nur mit entsprechenden
elektronischen Tricks möglich. Die entscheidende Idee dabei ist der
so genannte PRC ("Pseudo Random Code"). Ein vereinfachtes Beispiel
für Datenerkenung mittels PRC : Jeder der 24 Satelliten sendet
eine für ihn charakteristische Kennung. Sie besteht aus einer wohl
definierten aber in sich zufälligen Bitfolge aus N Bits, etwa
10100101001, die mit einer festen Frequenz, z.B. 1 MHz, ständig wiederholt
wird, z.B. so:
Sendersignal f1(t) = 1010010100110100101001101001010011010010100110100
usw..
Repräsentiert man die 1 als positive Spannung (+1)
, die 0 als negative Spannung (-1), so ergibt sich ein Stufensignal, das
im Takt des Binärcodes das Vorzeichen wechselt.
Um diese Bitfolge in dem vom Satelliten kommenden (in
der Praxis stark verrauschten) Datenstrom zu identifizieren, erzeugt der
Empfänger eben diese ihm bekannte Bitfolge intern ebenfalls als Signal,
aber zeitlich verschoben, also das Signal f2 =f1(t-t).
Für jede Zeitverschiebung t zwischen 0 und T werden nun beide Signale
über eine Periode T elektronisch multipliziert und summiert. Man bildet
also das "Faltungsintegral" ![]() F(t)
= f1(t) f1(t-t) dt. Sind die Bitfolgen
zeitlich korreliert , dann ergibt sich dabei hierbei ein großes positives
Ausgangssignal, ist das nicht der Fall, so ergibt wegen der Zufälligkeit
des Codes auch nur ein kleiner Zufallswert um 0. Findet man also
bei einem bestimmten Wert der Phasenverschiebung ein großes Ausgangssignal,
dann handelte es sich um den entsprechenden Satellit. Gleichzeitig ergibt
sich über die Phasenverschiebung selbst die zeitliche Korrelation
beider Signale, die für die Berechnung der Signallaufzeit benötigt
wird.
F(t)
= f1(t) f1(t-t) dt. Sind die Bitfolgen
zeitlich korreliert , dann ergibt sich dabei hierbei ein großes positives
Ausgangssignal, ist das nicht der Fall, so ergibt wegen der Zufälligkeit
des Codes auch nur ein kleiner Zufallswert um 0. Findet man also
bei einem bestimmten Wert der Phasenverschiebung ein großes Ausgangssignal,
dann handelte es sich um den entsprechenden Satellit. Gleichzeitig ergibt
sich über die Phasenverschiebung selbst die zeitliche Korrelation
beider Signale, die für die Berechnung der Signallaufzeit benötigt
wird.
Das Satellitensystem ist so aufgebaut, dass bei freier Sicht zu jeder Zeit und an jedem Ort der Erde die Signale von 4 bis 8 Satelliten empfangen werden können. Ein Empfänger kann aus der Laufzeit der vier Signale die momentane Position auf 5 m genau berechnen. Notwendig wäre zur Ortsbestimmung eigentlich nur der Empfang von drei Satelliten. Dann müsste der Empfänger aber selbst eine hoch präzise Atomuhr besitzen. Das ist nicht notwendig, denn das vierte Signal liefert die genaue Zeitkoordinate, mit der der Empfänger eine einfache Quarzuhr synchronisiert.
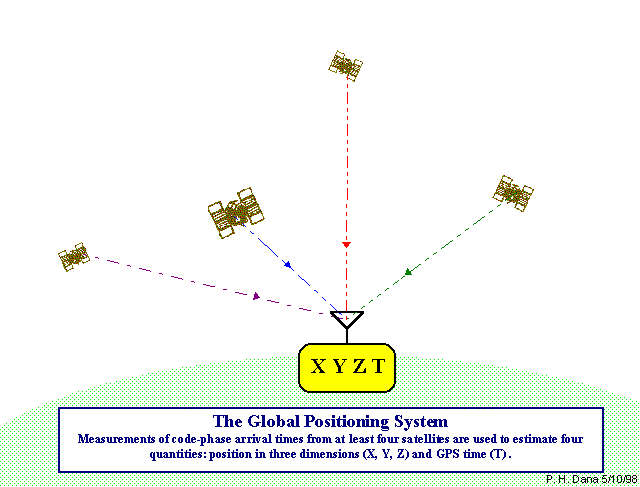
Das GPS funktioniert nur, weil die Lichtgeschwindigkeit
in allen Richtungen gleich ist.
Lange Zeit wurde das Satellitensignal vom US-Militär
so verändert, dass zivile Nutzer nur die "Selected Availability"
nutzen konnten. Die Genauigkeit der Positionen war zeitlich schwankend
und in der Regel nur auf etwa 100m genau. Am 1. Mai 2000 um 0 Uhr
wurde die "Selected Availability" auf Anregung des Kongresses
durch Bill Clinton "endgültig und für immer" ausgeschaltet.
Das Militär hat nämlich inzwischen die Möglichkeit, diese
Funktion auf regionaler Basis (z.B. in Konfliktfällen) zu aktivieren.
Seitdem ist die Genauigkeit der Positionen standardmäßig etwa
± 10m.
GPS liefert zunächst als Positionsangaben ECEF (Earth Centered, Earth Fixed) Kartesische Koordinaten X, Y, Z:
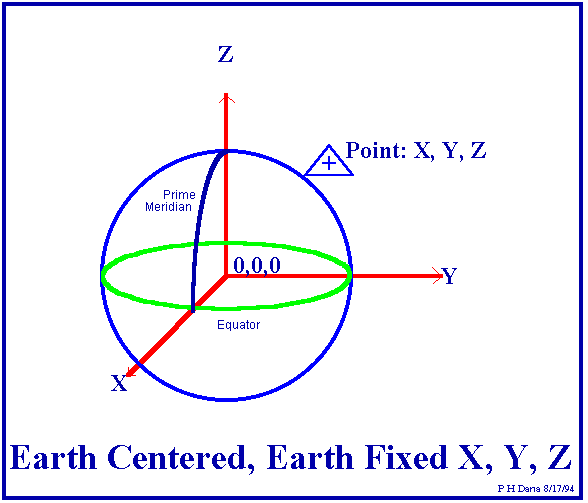
Der Ursprung des Koordinatensystems liegt im Zentrum des
Referenzellipsoids (s.u.), die Z-Achse zeigt zum Nordpol, die X-Achse zum
Schnittpunkt der Äquatorebene mit dem Nullmeridian und die Y-Achse
senkrecht zu beiden.
Hier ein Beispiel für die ECEF-Koordinaten:

Die geografischen Koordinaten, die in Karten benutzt werden, müssen aus diesen Koordinaten erst berechnet werden. Hierzu benötigt man ein Erdmodell, bei dem die wahre Gestalt der Erde in der Regel durch ein Ellipsoid angenähert wird.
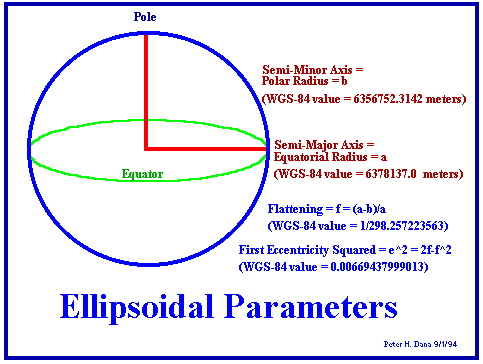
Alle Koordinatenangaben haben deshalb nur einen Sinn, wenn das dazugehörige Referenzellipsoid bekannt ist. Dazu muss die große Halbachse a (der Äquatorradius) und die kleine Halbachse b (der Polradius) oder die große Halbachse und die Abplattung f=(a-b)/a gegeben sein.
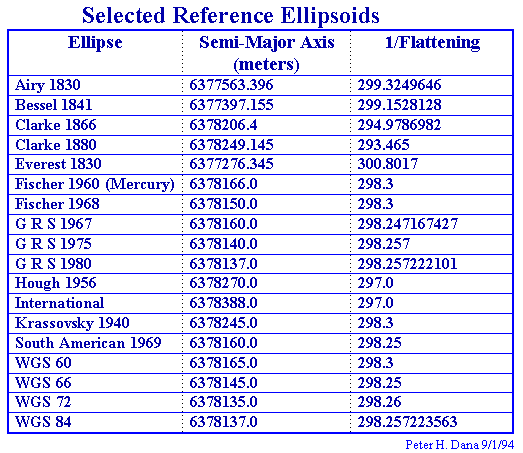
Oft werden die Datumsangaben relativ zum WGS-Ellipsoid gemacht (WGS-84: Äquatorradius a = 6378137.0 km, Abplattung f = 1/298.257223563), die Tabellenangabe
Potsdam_Rauenberg_DHDN, Bessel_1841, 739.845, 0.10037483, +606, +23, +413
z.B. bedeutet:
Name: Potsdam_Rauenberg_DHDN
Name des verwendeten Ellipsoids: Bessel_1841
a - a' = 739.845 m (Differenz der Äquatorrradien)
f - f ' = 0.10037483 × 10-4 (Differenz der
Abplattung)
Dx = +606m
Dy = +23m
Dz = +413 (Verschiebungen des Mittelpunkts des
Referenzellipsoids gegenüber dem WGS84-Ellipsoid)
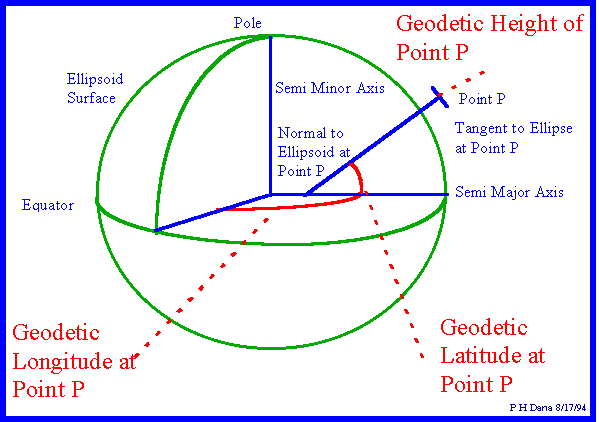
Die geografische Länge eines Punkt P ist dann der Winkel zwischen der Ebene des Nullmeridians und der Ebene, die durch den Punkt P und den Pol geht und senkrecht auf dem Äquator steht, die geografische Breite der Winkel zwischen dem Äquator und der Flächennormalen des Ellipsoids beim Punkt P. Die geodätische Höhe ist der senkrechte Abstand des Punktes P vom Referenzellipsoid.
Die besten Erdmodelle dieser Art können die wahre Erdoberfläche, repräsentiert durch die mittlere Meeresoberfläche, auf wenige hundert Meter genau modellieren. Die gelingt aber nur regional, d.h. der gewählte Ellipsoid ist nur für bestimmte Bereiche der Erdoberfläche optimal. Daher gibt es sehr viele solcher geodätischen Systeme ("Datums"). Die topografischen Karten der deutschen Landesvermessungsämter benutzen das Rauenberg-Potsdam-Datum. Standardmäßig werden die Koordinaten vom GPS12 im WGS84-Datum angezeigt. Stellt man das GPS nicht richtig ein, so kann das zu erheblichen Fehlern führen.
Hier die Koordinaten für den Haupteingang der Schule
in verschiedenen geodätischen Systemen:
| Datum | Länge | Breite |
| POTSDAM/RAUENBERG | 50° 55,613' N | 7° 16,760 E |
| WGS84 | 50° 55,537 N | 7° 16,710 E |
| AUSTRIA | 50° 55,593 N | 7° 16,701 E |
| CH-1903 | 50° 55,645 N | 7° 16,770 E |
| EUROPEAN 1979 | 50° 55,585 N | 7° 16,784 E |
| IRELAND 1979 | 50° 55,491 N | 7° 16,868 E |
| NAD-83 | 50° 55,537 N | 7° 16,710 E |
Die Karte zeigt, dass man diese Differenzen keineswegs vernachlässigen darf: Die Abweichungen können in ungünstigen Fällen bis zu 1 km betragen:
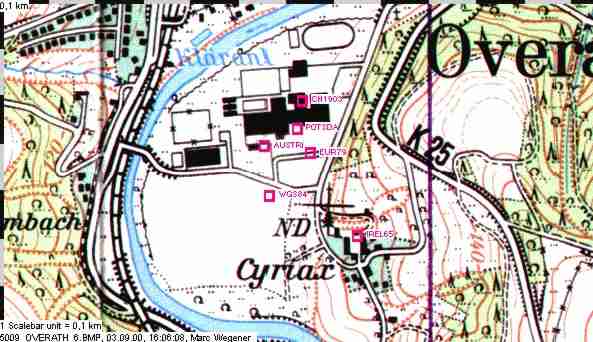
Die Positionen für den Haupteingang des Paul-Klee-Gymnasiums in verschiedenen geodätischen Systemen
Während GPS12 intern alle Koordinaten in WGS84 speichert, kann die Anzeige wahlweise in etwa 100 verschieden Daten erfolgen. Die notwendigen Datumskonversionen sind intern programmiert. Hier die Formeln zur Umrechnung von ECEF-Koordinaten in Koordinaten eines bestimmten Datums und umkgekehrt:


Die Höhenangaben bedürfen besonderer Sorgfalt bei der Interpretation. Hierbei sind verschiedene "Erdoberflächen" zu unterscheiden.
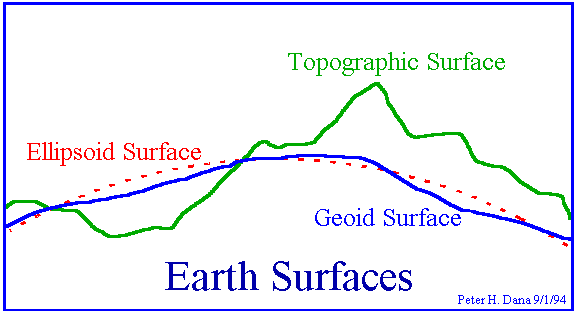
Die topografische Oberfläche ist die tatsächliche
Oberfläche von Land oder Meer zu einem bestimmten Zeitpunkt.
Die Ellipsoidoberfläche ist die Oberfläche
des verwendeten Referenzellipsoids. Der Normalpegel (Meereshöhe)
entspricht der mittleren Meereshöhe, wobei es wiederum viele unterschiedliche
Methoden der Mittelwertbildung gibt. Gezeitenkräfte und lokale Unterschiede
der Gravitation führen dazu, dass selbst diese Oberfläche sich
in verschieden Gegenden der Erde um hunderte Meter unterscheiden kann.
Die Geoidoberfläche ist die Fläche gleichen Gravitationspotentials:
Ein Pendel richtet sich lokal immer genau senkrecht zu dieser Fläche
ein. Durch Einflüsse aus dem Erdinnern (unterschiedliche Dichteverteilungen)
und der Erdoberfläche (Gebirge) ist auch diese Fläche unregelmäßig
geformt.
GPS gibt immer die geodätische Höhe relativ
zum verwendeten Ellipsoid an.
Neben unterschiedlichen Daten werden in der Geodäsie auch sehr verschiedene Koordinatensysteme verwendet. Hier eine kleine Übersicht, dargestellt anhand eines bestimmten topografischen Punktes der USA (der Stern in der Hand der Freiheitsgöttin auf der Spitze des Kapitols in Austin/Texas):
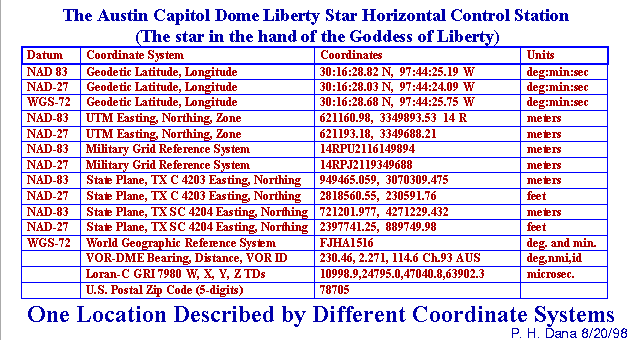
Neben den bekannten Gradangaben ( dd° mm' ss" oder dd° mm,mmm' ) werden vor allem bestimmte Zonennetze verwendet. International verwendet wird z.B. ist das UTM-Gitter. Daneben existieren eine Unzahl von nationalen Gittern, in Deutschland z.B. die Gauß-Krüger-Koordinaten, in der Schweiz das Schweizer Netz.
Das UTM-Gitter (UTM = Universal Transverse Mercator) definiert zweidimensionale horizontale Positionen. Die UTM-Zonen-Nummern bezeichnen 6° breite longitudinale Streifen von 80° Süd bis 84° Nord. Die UTM-Zonen-Bezeichner kennzeichnen 8° breite Breitenstreifen. Nördlich von 72° gibt es einige Sonderzonen unterschiedlicher Breite.
Jede Zone hat einen Zentralmeridian, die Zone 32U in Deutschland
z.B. den 9. Längengrad. Sie erstreckt sich also 6° E
bis 12° E.
Die Ostwerte im UTM-System werden in Meter von diesem
Zentralmeridian aus gemessen, wobei 500km addiert werden ("false easting"),
damit sich immer nur positive Werte ergeben. Die Nordwerte werden ebenfalls
in Meter vom Äquator aus gemessen (mit 10000km "false northing" für
Punkte südlich des Äquators).
Beispiel: PKG-Haupteingang :
Potsdam
50° 55,613' N 7° 16,760 E
UTM 32U 0379090
5642524
GARMIN GPS12
Der kleinste und handlichste Empfänger für den privaten Gebrauch aber mit allen wichtigen Navigationsfunktionen. Preis z.Zt. (8/2000) ca. 350,00 DM. Das Gerät wird mit 4 Mignonzellen betrieben.

Beim Einschalten sucht GPS12 zunächst den Himmel nach Satelliten ab. Die Satellitenseite zeigt neben der Batterieanzeige die über dem Horizont befindlichen Satelliten und ihre Nr. an. Ihre Position am Himmel kann an der Kalotte (Horizont und 45°-Höhenlinie) abgelesen werden. Das Balkendiagramm zeigt die Empfangsstärke an und ob der Satellit zur Positionsberechnung benutzt wird. Hat der GPS12 eine gültige Position berechnet, dann zeigt er oben links, ob es sich um eine 2D-Position oder eine 3D-Position mit Höhe handelt sowie den EPE (Estimated Positional Error = geschätzter Positionsfehler) in m.

Satelliten-Seite
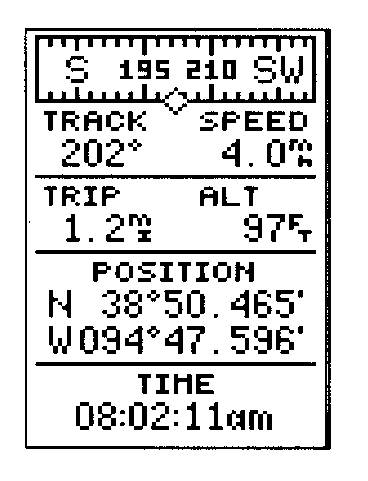
Positions-Seite
GPS12 springt dann auf die Positionsseite und zeigt die Koordinaten und die Höhe im eingestellten System. Bewegt man sich weiter, dann wird die Geschwindigkeit und die Richtung der momentanen Bewegung angezeigt. "Trip" zeigt die seit der letzten Rückstellung gegangene Strecke. Darüber hinaus gibt das Gerät die genaue Zeit an.
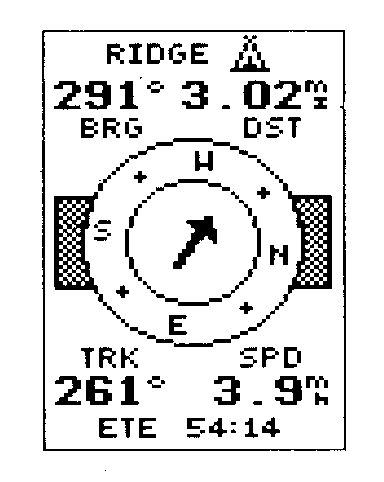
Navigationsseite
Die Navigationsseite wird benutzt, um mit der "GO-TO"-Funktion einen Wegpunkt anzulaufen. Es lassen sich bis zu 500 Wegpunkte mit Namen eingeben und speichern. Mit der "MARK"-Funktion wird der augenblickliche Standort automatisch als Wegpunkt gespeichert. Die Kompassrose der Navigationsseite zeigt oben den Azimut der momentanen Bewegung an (TRK = track) , der Richtungspfeil die Sollrichtung zum Zielpunkt (BRG = bearing). Daneben kann man sich den Abstand zum Zielpunkt, die Momentangeschwindigkeit und die geschätzte Ankunftszeit angeben lassen.
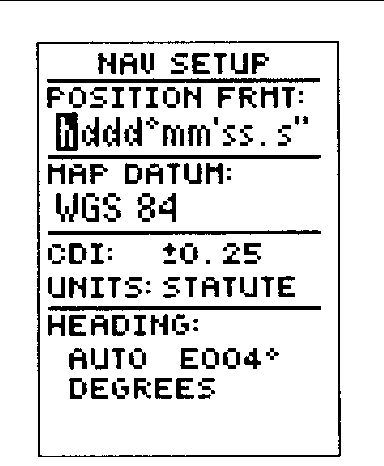
Setupseite
In zahllosen Setup-Seiten lassen sich die wichtigsten
Navigationsparameter einstellen. "Position Format" ist z.B. das
gewünschte Koordinatensystem (Grad, UTM, German Grid = Gauß-Krüger,
Swiss Grid = Schweizer Netz der Schweizer Landeskarten usw.), "Map Datum"
der Referenzellipsoid. Etwa 100 verschiedene Datums sind wählbar,
mit USER-defined aber auch jedes beliebige andere Datum.
Der GPS12 verfügt weiter über die Möglichkeit,
den Weg (Track) automatisch aufzuzeichnen. In vorwählbaren
Zeitintervallen oder auch automatisch werden bis zu 1024 Trackpunkte im
Gerät abgelegt, die sich später auslesen lassen.
Bis zu 30 Wegpunkte lassen sich in einer von 19 "Routen"
abspeichern. Bei eingestellter Route zeigt GPS12 immer den Weg zum nächsten
Wegpunkt und springt beim Erreichen automatisch zum nächsten Wegpunkt
weiter.
Eine weitere Funktion ist TrackBack: Sie ermöglicht
es, den aufgezeichneten Weg sofort zurückzugehen. Die Trackpunkte
des aufgezeichneten Tracks werden dabei automatisch in einer Route abgelegt.
GPS12 verfügt über eine Schnittstelle zum seriellen Port eines PC. Mit entsprechender Software lassen sich Wegpunkte und Routen verwalten, Koordinaten aus gescannten Karten einlesen, speichern und in das GPS12 übertragen, ebenso funktioniert natürlich der Datentransfer in umgekehrter Richtung. Abgegangene Tracks lassen sich z.B. nachträglich auf der Karte betrachten.
Ich benutze z.Zt. das Programm QUOVADIS 1.62C (Internet: www.quovadis-gps.com). Hiermit lassen sich praktisch alle anfallenden Navigationsaufgaben, Umrechnungen, Kartenarbeiten usw. bewerkstelligen. Neben den gängigen digitalen Kartenformaten arbeitet das Programm auch mit gescannten Daten aus vorhandenem Kartenmaterial reibungslos zusammen.